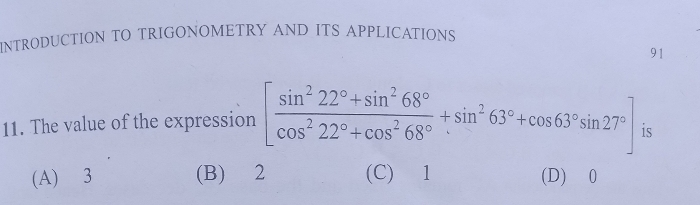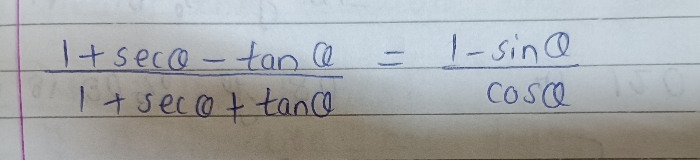Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

show that 6(sinx+cosx)p4+12(sinx-cosx)p2+8(sinp6x+cosp6x)=26 where p4,p2,p6are use for power4,power2(square),power6
Asked by | 24 Aug, 2012, 03:37: PM
answered-by-expert Expert Answer
6(sinx+cosx)4+12(sinx-cosx)2+8(sin6x+cos6x)
= 6(sin2x+cos2x+2sinxcosx)2+12(sin2x+cos2x-2sinxcosx)+8(sin2x+cos2x)3 - 24sin2xcos2x(sin2x+cos2x)
= 6(1+2sinxcosx)2+12(1-2sinxcosx)+8 -24sin2xcos2x
= 6(1+4sin2xcos2x+4sinxcosx)+12(1-2sinxcosx)+8 -24sin2xcos2x
= 6+24sin2xcos2x+24sinxcosx+12-24sinxcosx+8 -24sin2xcos2x
= 26
 
Hence, proved.
Answered by | 26 Aug, 2012, 11:28: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
cos80÷ sin10+cos59• cosec31
Asked by raopaidi | 25 Apr, 2024, 04:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
ABCD is a rectangle in which diagonal AC is equals to 17 cm angle BCA is equals to thitha and sin theta is equals to 8/17 find the area of rectangle ABCDE (ii) the perimeter of rectangle ABCD
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
the poles AB and CD of different heights are standing vertically on the ground level from a point P on the line joining the foots of the pole on the level of ground the angle of elevation to the top of the pole are founded to be complementary the of the CD and the distance PD 20√3m and 20m respectively if the BP is 10m then find the length of AB and the distance AC between the tpo of the poles
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
√1+sin A/√1-sin A
Asked by vn3950372 | 18 Mar, 2024, 08:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
from the top of your vertical building of 350 m height on a level ground the angle of depression on of an object on the same ground is observed to be 60 degree find the distance of the object from the foot of the building
Asked by jayashreelatha04 | 17 Mar, 2024, 05:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
trigonometry
question image
Asked by vk952384 | 09 Mar, 2024, 11:34: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the value of cos20 if 2sin20 is root 3
Asked by gauravgupta.20008 | 03 Feb, 2024, 05:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
6. A is an acute angle in right triangle, right angled at B then value of (sinA + CosA) is ( a) Greater than (b) less than 1 (c) equal to 1 (d) depends on value of A
Asked by sathwicksathwick06 | 01 Feb, 2024, 07:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
solution
question image
Asked by pankajmali55 | 25 Jan, 2024, 07:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Q1. Ina DABC, LB=90^{\circ} If AB=2cm and AC=3cm Find Sin A.
Asked by tanujmaan58 | 18 Jan, 2024, 08:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×