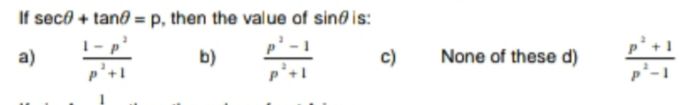CBSE Class 10 Answered
question
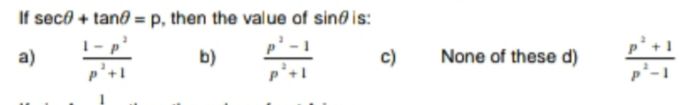
Asked by arindeep.singh | 10 Sep, 2020, 19:04: PM
Given: sec theta + tan theta = p
TO find: sin theta
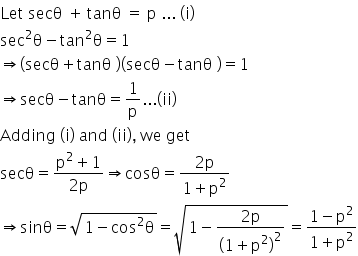
Answered by Renu Varma | 10 Sep, 2020, 19:48: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 18:44: PM
CBSE 10 - Maths
Asked by priyanshdhiman2008 | 25 Dec, 2023, 15:12: PM
CBSE 10 - Maths
Asked by deepakverma786024 | 18 Dec, 2022, 05:43: AM
CBSE 10 - Maths
Asked by Bavashreelogasundaram | 22 Sep, 2022, 20:26: PM
CBSE 10 - Maths
Asked by sahanahosamani2005 | 25 Nov, 2020, 22:58: PM
CBSE 10 - Maths
Asked by choudharylakshay786 | 16 May, 2020, 12:56: PM
CBSE 10 - Maths
Asked by kssvsv2011 | 09 May, 2020, 20:44: PM
CBSE 10 - Maths
Asked by gurunath196107 | 07 Apr, 2020, 16:21: PM