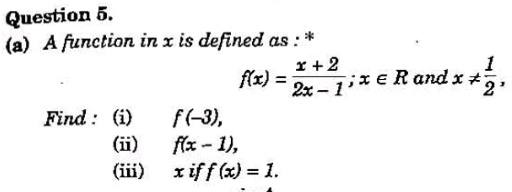ICSE Class 10 Answered
Q.14
Asked by kaivankoshti7111.10sdatl | 06 Jul, 2020, 08:56: PM
Expert Answer
TO find the remainder os the polynomial using remainder theorem.
Given polynomial is P(x)=x3+(kx+8)x+k
When P(x) is divided by x+1 and x-2, the remainders would be P(-1) and P(2)
P(-1) = (-1)3 + [k(-1) + 8](-1) + k = -1 + k - 8 + k = 2k - 9
P(2) = (2)3 + [k(2) + 8](2) + k = 8 + (2k + 8)2 + k = 8 + 4k + 16 + k = 5k + 24
Sum of these two remainders is 1
Therefore, 2k - 9 + 5k + 24 = 1
5k + 2k + 24 - 9 = 1
7k + 15 = 1
7k = -14
k = -2
Answered by Renu Varma | 07 Jul, 2020, 11:18: AM
Concept Videos
ICSE 10 - Maths
Asked by madhab_chaudhuri | 06 Dec, 2022, 01:38: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by tanaypatidar12345 | 25 Mar, 2022, 03:56: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by yogiy7984 | 08 Oct, 2020, 08:53: AM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by santoshverma080285 | 20 Aug, 2020, 03:17: PM
ANSWERED BY EXPERT
ICSE 10 - Maths
Asked by armantiwari07.10spicertl | 23 May, 2020, 04:35: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by armantiwari07.10spicertl | 23 May, 2020, 04:35: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by ramasareverma99 | 13 May, 2020, 04:42: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by kushalsahu20march | 16 May, 2019, 11:56: AM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by rajatpullinacd | 15 May, 2019, 04:35: PM
ANSWERED BY EXPERT
