CBSE Class 11-science Answered
Q10
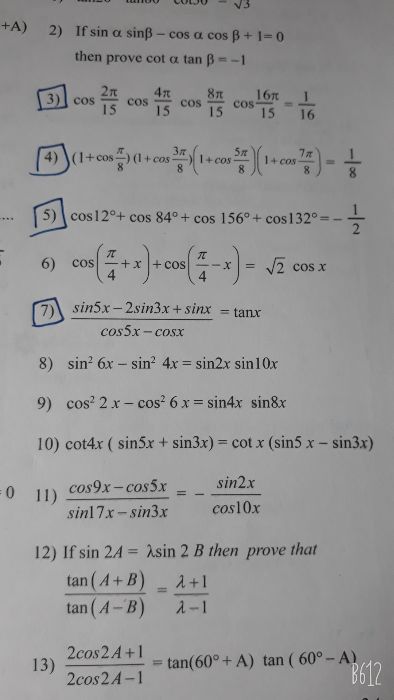
Asked by omved0304 | 07 Aug, 2020, 11:24: AM
To prove that cot 4x (sin 5x + sin 3x) = cot x (sin 5x - sin 3x)
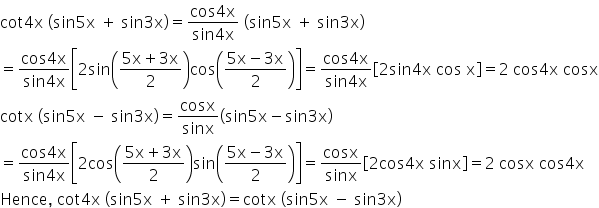
Answered by Renu Varma | 11 Aug, 2020, 12:08: PM
Concept Videos
CBSE 11-science - Maths
Asked by bimanmandal53361 | 15 Jan, 2024, 00:32: AM
CBSE 11-science - Maths
Asked by mishraparveen1234 | 15 Jun, 2022, 16:56: PM
CBSE 11-science - Maths
Asked by shanujam03 | 03 Oct, 2020, 20:59: PM
CBSE 11-science - Maths
Asked by richasingh0708.bmps | 23 Jun, 2020, 22:00: PM
CBSE 11-science - Maths
Asked by dppanigrahiadv | 26 May, 2020, 19:03: PM
CBSE 11-science - Maths
Asked by lykanbeast04 | 21 May, 2020, 18:49: PM
CBSE 11-science - Maths
Asked by Singhnitish1475 | 11 May, 2019, 01:46: AM





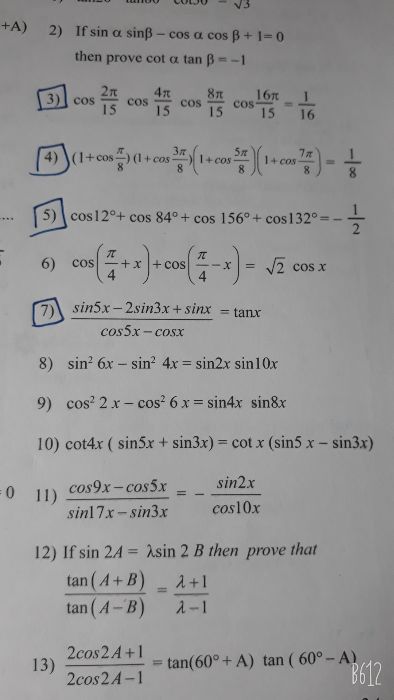
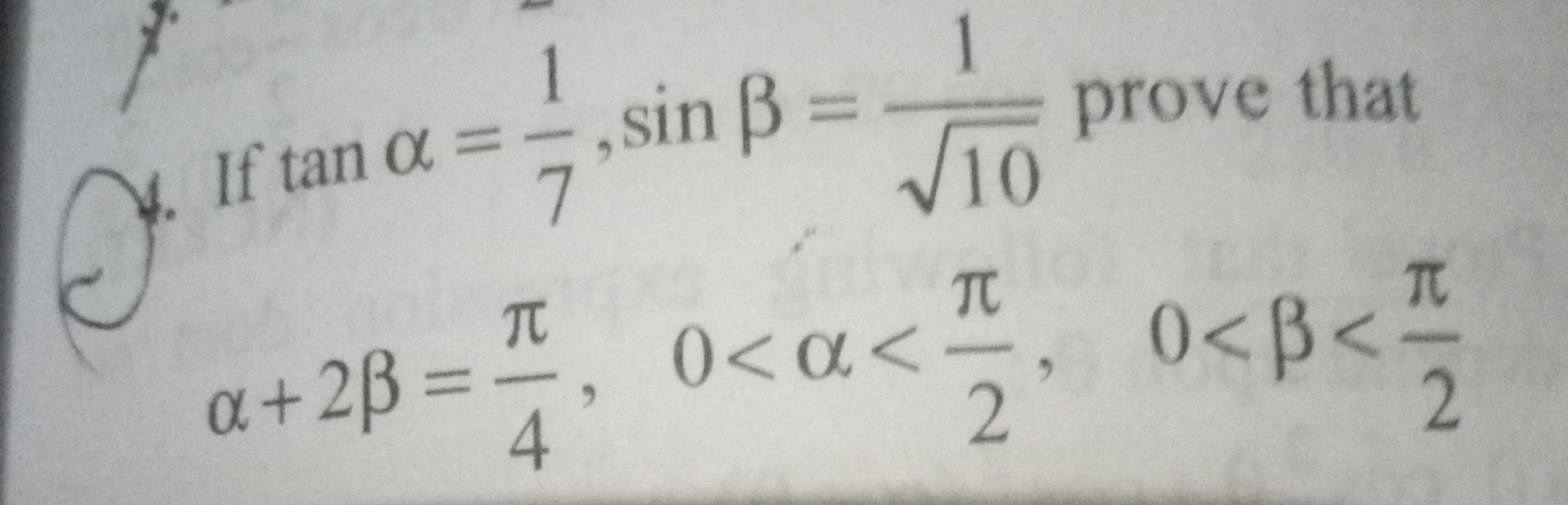
 ,then what is the value of cosec(7
,then what is the value of cosec(7