CBSE Class 11-science Answered
prove that in an elastic one dimensional collision between two bodies, the relative velocity of approach before collision is equal to the relative velocity of seperation after the collision. Hence derive expressions for the velocities of two bodies in terms of their initial velocities before collision.
Asked by shafiaagha999 | 27 Feb, 2020, 23:40: PM
• The collision in which both the momentum and kinetic energy are conserved and the colliding bodies continue to move along the same straight line after the collision is called an elastic collision in one dimension.
• Let two perfectly elastic bodies A and B of masses m1 and m2, moving along the same straight line with velocities u1 and u2, respectively.
• The two bodies will collide only if u1 > u2. The difference in initial velocities i.e., (u1 - u2) is called velocity of approach.
• Two bodies undergo a head-on collision and continue moving along the same straight line with velocities v1 and v2 in the same direction.
• The bodies will separate after collision only if v2 > v1.
The difference in final velocities i.e., (v2 > v1) is called velocity of separation.
• According to the law of conservation of momentum,
m1 u1 + m2 u2 = m1 v1 + m2 v2 ... (1)
m1 (u1 - v1) = m2 (v2 - u2) ... (2)
Substituting v2 in eqn. (1), we get,
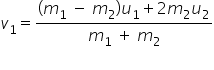 ... (3)
... (3)• According to the law of conservation of kinetic energy,

m1 (u12 - v12) = m2 (v22 - u22) ... (4)
Dividing eqn. (1) and (2), we get,
u1 - u2 = v2 - v1 ...(5)
From eqn. (3), it follows that in one dimensional elastic collision, the relative velocity approach (u1 - u2) before collision is equal to the relative velocity of separation (v2 - v1) after collision.
Substituting v2 in eqn.(5), we get,
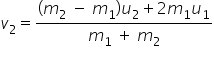 ... (6)
... (6)• Calculating the final velocities of the two bodies after collision:
When the two bodies are of equal masses:
Consider that, m1 = m2 = m
From eqn. (3), we get,
v1 = u2
From eqn. (5),
From eqn. (5),
we get,
v2 = u1
Thus, if two bodies of equal masses suffer elastic collision in one dimension, then after the collision, the bodies will exchange their velocities.
Thus, if two bodies of equal masses suffer elastic collision in one dimension, then after the collision, the bodies will exchange their velocities.
Answered by Shiwani Sawant | 28 Feb, 2020, 11:08: AM
Concept Videos
CBSE 11-science - Physics
Asked by duraisamysteephen | 08 Jun, 2024, 12:32: PM
CBSE 11-science - Physics
Asked by KRISHPATEL.soc | 22 Apr, 2022, 16:19: PM
CBSE 11-science - Physics
Asked by unnatibhise08 | 22 Dec, 2021, 08:46: AM
CBSE 11-science - Physics
Asked by arjunsah797 | 21 Jun, 2021, 06:57: AM
CBSE 11-science - Physics
Asked by shafiaagha999 | 27 Feb, 2020, 23:40: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 15 Jul, 2014, 11:21: AM
CBSE 11-science - Physics
Asked by Topperlearning User | 15 Jul, 2014, 11:22: AM
CBSE 11-science - Physics
Asked by Topperlearning User | 15 Jul, 2014, 11:23: AM





