CBSE Class 10 Answered

1)Let us assume that   is a rational;  where a and b are co prime,                        

so,b =a                                                                                                            

So,  squaring both sides, we get

 _5b²  _{= a}²                                                                               

Therefore a² is dividable by 5 and also a is divisible by 5.   

Now we can write a=5c  for some integer c.             

Substituting this value of for a, in (1) we get

5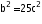 i.e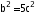 

This means that  is divisible by 5 and also b is divisible by 5.  Therefore a and b have 5 as their common factor, but this contradicts the fact that a and b are co prime.  The contradiction arises because of our wrong assumption that  is a rational.                

 So, we conclude that  is an irrational.

Suppose 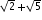 is not an irrational number, then it must be a rational number.

So let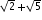 =q where q is a rational number.

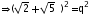
2+5+2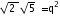

So here we have an equation with its   left side is a rational number(as the set of rational numbers is closed under subtraction and division i.e the subtraction and division of two rational numbers is always a rational number)and  so its right side must also be a rational number.

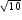 is a rational number

Which is a   contradiction. So our basic assumption   must be wrong.

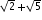=q where q is a rational number,is wrong

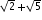 is an irrational number.

Hence proved.

similarly we can prove the other parts.