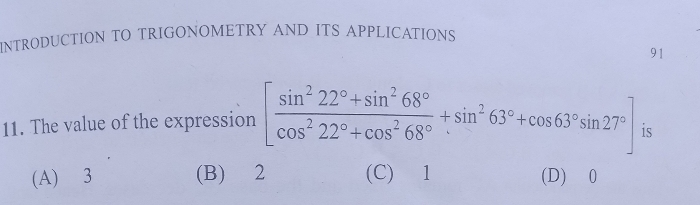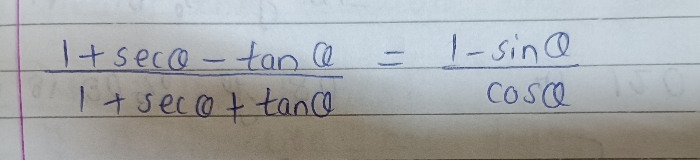CBSE Class 10 Answered
prove that
1/(sec x -tan x)-1/cos x = 1/cos x - 1/(sec x + tan x )
Asked by | 10 Aug, 2012, 05:47: PM
LHS = 1/(sec x -tan x)-1/cos x
= sec x + tan x/(sec x - tan x)(sec x + tan x) - 1/cos x
= sec x + tan x/(sec2x - tan2x) - 1/cos x
= sec x + tan x - sec x
= tan x
RHS = 1/cos x - 1/(sec x + tan x)
= 1/cos x - (sec x - tan x)/(sec x + tan x) (sec x - tan x)
= 1/cos x - (sec x - tan x)/(sec2x - tan2x)
= sec x - (sec x - tan x)/1
= sec x - sec x + tan x
= tan x
Hence, LHS = RHS
Answered by | 10 Aug, 2012, 09:31: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by raopaidi | 25 Apr, 2024, 04:06: PM
CBSE 10 - Maths
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by jayashreelatha04 | 17 Mar, 2024, 05:38: PM
CBSE 10 - Maths
Asked by gauravgupta.20008 | 03 Feb, 2024, 05:36: PM
CBSE 10 - Maths
Asked by sathwicksathwick06 | 01 Feb, 2024, 07:30: PM
CBSE 10 - Maths
Asked by tanujmaan58 | 18 Jan, 2024, 08:47: PM