CBSE Class 9 Answered
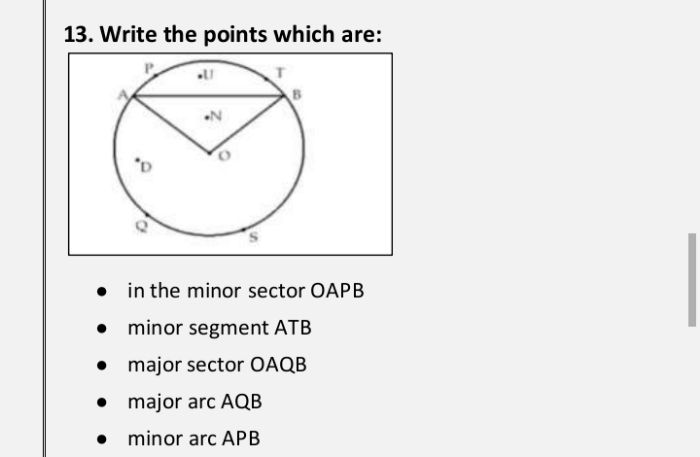
Plz help me with this .
Asked by | 01 Jan, 2013, 11:15: PM

![]() ABC is an equilateral triangle.
ABC is an equilateral triangle.
AB = BC = CA = 9 cm
O is the circumcentre of ![]() ABC.
ABC.
![]() OD is the perpendicular bisector of the side BC.
OD is the perpendicular bisector of the side BC.
(O is the point of intersection of the perpendicular bisectors of the sides of the triangle)
In ![]() OBD and
OBD and ![]() OCD,
OCD,
OB = OC (Radius of the circle)
BD = DC (D is the mid point of BC)
OD = OD (Common)
![]()
![]() OBD
OBD ![]()
![]() OCD (SSS congruence criterion)
OCD (SSS congruence criterion)
![]()
![]() BOD =
BOD = ![]() COD (CPCT)
COD (CPCT)
![]() BOC = 2
BOC = 2 ![]() BAC
BAC
= 2 × 60°
= 120° ( The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle)

In ![]() BOD,
BOD,
Sin ![]() BOD
BOD ![]()

Answered by | 03 Jan, 2013, 11:32: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by indu.suresh1220 | 27 Dec, 2023, 11:12: PM
CBSE 9 - Maths
Asked by subbusuchi1978 | 05 Nov, 2023, 10:24: AM
CBSE 9 - Maths
Asked by rameshsonkar1234ramesh | 21 Dec, 2022, 11:03: PM
CBSE 9 - Maths
Asked by sdmbotch1123 | 17 Dec, 2022, 09:39: PM
CBSE 9 - Maths
Asked by geetaradha8835 | 16 Dec, 2022, 07:59: PM
CBSE 9 - Maths
Asked by chalkekalyani80 | 06 Mar, 2022, 11:25: AM
CBSE 9 - Maths
Asked by sangeetabharti123456789 | 22 Feb, 2022, 09:01: AM
CBSE 9 - Maths
Asked by manognareddy.p28 | 25 Jul, 2021, 12:52: PM
CBSE 9 - Maths
Asked by Samidhaindulkar133 | 11 Mar, 2021, 04:03: PM