CBSE Class 9: Properties of Equal Chords Videos | Properties of Equal Chords
Properties of Equal Chords
This video explains the results on equal chords and their distance from the centre and also solves problems based on these results.
More videos from this chapter
View All-
Concepts on angle subtended by a chord at a point ...
-
Properties of Equal Chords
-
Relation between angle subtended by an arc at centre ...
-
Angle subtended by a chord at a point
-
Properties ...
-
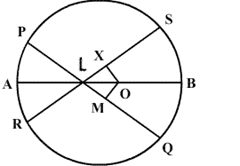
If two intersecting chords PQ and RS of a circle make equal angles with the diameter passing through their point of intersection, then prove that the chords are equal.
-
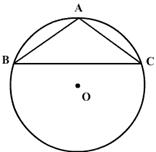
Prove that the angle in the minor segment is an obtuse angle.
-
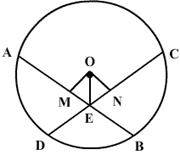
In the given figure, equal chords AB and CD of a circle C(O, r) cut at right angles at E. If M and N are the mid points of AB and CD respectively, prove that OMEN is a square.
-
In the figure A, B and C are three points on a circle such that the angle subtended by the chords AB and AC at the centre are 120o and 80o respectively. Determine angle BAC.
-
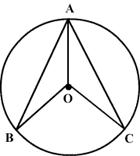
P is the centre of the circle. Prove that
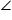XPZ is equal to twice the sum of 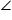XZY and 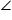YXZ.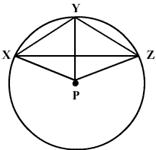 
-
O is the centre of the circle, find the value of x.
-
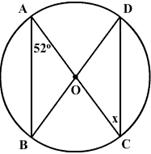
AB and AC are two equal chords of a circle whose centre is O. If OD is perpendicular to AB and OE is perpendicular to AC, prove that
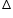ADE is an isosceles triangle. 
-
O is the centre of the circle and PQ is a diameter. If 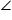ROS is equal to 40o find 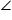RTQ.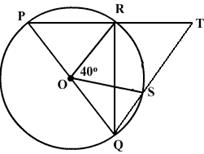
-
PQ and RQ are the two chords of a circle equidistant from the centre O. Prove that the diameter passing through Q bisects 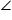PQR and 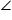PSR.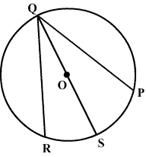
-
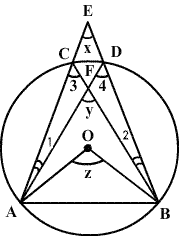
In the figure, O is the centre of a circle. Prove that x + y = z.
