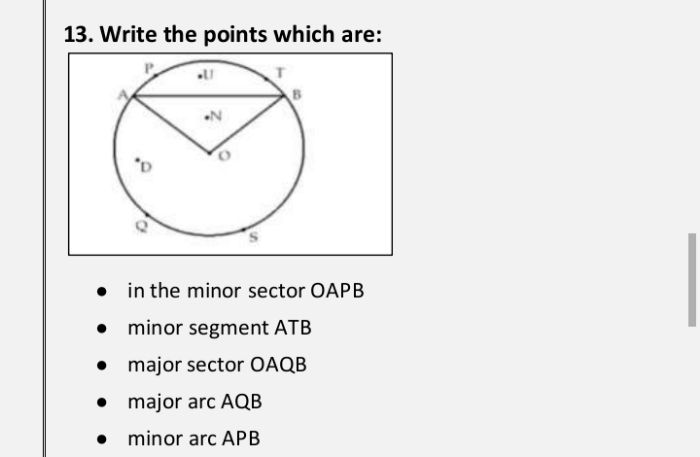
CBSE Class 9 Answered

assume that two equal chords AB,CD of a circle  intersect at P.

Let O be the center of the circle.

drop OM,ON perpendiculars from O to AB,CD respectively.

since perpendicular from the center bisects a chord,

so Mand N become the mid points of AB,CD respectively.

i.e.AM=MB

and

CN=ND

now,

consider  right triangles OPN,OPM

OP=OP common side

OM=ON... equal chords are equidistant from the center

so OPN cong to OPM... RHS rule.

PN=PM...CPCT.

now,

NC=AM=DN=MB.. since the chords are equal, their half parts also are equal.

so taking,

NC=AM,

we get,

NP+PC=AP+PM

but PM=PN, proved above,

so

PC=AP

simly,

DN=MB

hence proved.