Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

let the equations be x^2+x+2=0 and ax^2+bx+1=0 have atleast one common root then a+b equals to
Asked by sandeepkumarbhadauria41 | 15 Sep, 2021, 14:52: PM
answered-by-expert Expert Answer
Given equations are
 
x2 + x + 2 = 0   ...........................(1)
 
a x2 + b x + 1 = 0  ........................(2)

 
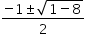
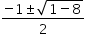
Roots of Eqn.(1) :- begin mathsize 14px style fraction numerator negative 1 plus-or-minus square root of 1 minus 8 end root over denominator 2 end fraction end style 
 
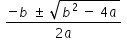
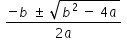
Roots of Eqn.(2)  :-    begin mathsize 14px style space fraction numerator negative b space plus-or-minus space square root of b squared space minus space 4 a end root over denominator 2 a end fraction space end style
if both equations have a common root , then  -b/(2a) = -1/2   or  b = a
 
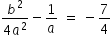
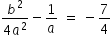
Also begin mathsize 14px style fraction numerator b squared over denominator 4 a squared end fraction minus 1 over a space equals space minus 7 over 4 end style
if we substitute b =a in above expression, we get a = (1/2) after simplification
 
Hence we have , a = b = 1/2    or  a+b = 1
Answered by Thiyagarajan K | 20 Sep, 2021, 21:50: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
ax^2+bx+c=0 then x=
Asked by manjushakothavade1979 | 25 Jun, 2024, 10:29: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
For a real number r, the quadratics x² + (r - 1) x + 6 and x² + (2r + 1) x + 22 have a common real root. The sum of the possible values of r can be expressed as a/ b where a, b are relatively prime positive integers. Compute 10a + b
Asked by Bhaveshkr211 | 30 Jul, 2023, 17:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Pls solve
question image
Asked by sdmbotch1123 | 18 Jan, 2023, 23:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
complete solution set of the equation |x^2-3|+|2-x|=|x^2-x-1|
Asked by rajshekhara348 | 20 Jun, 2022, 23:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
let the equations be x^2+x+2=0 and ax^2+bx+1=0 have atleast one common root then a+b equals to
Asked by sandeepkumarbhadauria41 | 15 Sep, 2021, 14:52: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Please solve all of these questions with proper explanation
question image
Asked by Suchismitasingha18 | 07 Aug, 2021, 16:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
questions 6
question image
Asked by sohailsidmd002 | 11 Oct, 2020, 14:35: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
find the value of p and q if the equation px²+5x+2=0 and 3x²+10x+q=0 have both roots in common.
question image
Asked by ssroul.tcbls | 02 Jul, 2020, 19:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
   the equation x minus 2 to the power 2 + x - 2 - 2 = 0 has how many roots
Asked by avinashjha3012 | 22 Jun, 2020, 17:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
The quadratic equation, who's roots are reciprocal of the roots of the equation- ax^2+bx+c,is?
Asked by drhimasingh | 26 May, 2020, 23:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Are You a Teacher or a Parent Seeking Customised Tests? Click here
×