CBSE Class 11-science Answered
Let L = 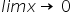 (a - (a - 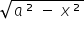 - x²?4) ÷ (x² × x²) , a > 0 . If L is finite , then (a) a = 2 , (b) a = 1 , (c) L = 1?64 , (d)L = 1/32 - x²?4) ÷ (x² × x²) , a > 0 . If L is finite , then (a) a = 2 , (b) a = 1 , (c) L = 1?64 , (d)L = 1/32 |
Asked by yeeshuraj3 | 28 Jul, 2016, 15:46: PM

Answered by Vijaykumar Wani | 29 Jul, 2016, 13:07: PM
Concept Videos
CBSE 11-science - Maths
Asked by akankhyapradhan123 | 18 Jan, 2022, 06:16: AM
CBSE 11-science - Maths
Asked by dineshchem108 | 02 May, 2019, 21:00: PM
CBSE 11-science - Maths
Asked by dineshchem108 | 01 May, 2019, 19:09: PM
CBSE 11-science - Maths
Asked by dineshchem108 | 16 Apr, 2019, 22:58: PM
CBSE 11-science - Maths
Asked by Shivendra | 23 Oct, 2018, 22:18: PM
CBSE 11-science - Maths
Asked by lovemaan5500 | 20 Jul, 2018, 18:12: PM
CBSE 11-science - Maths
Asked by lovemaan5500 | 17 Jul, 2018, 18:06: PM




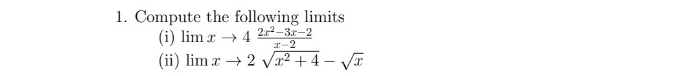
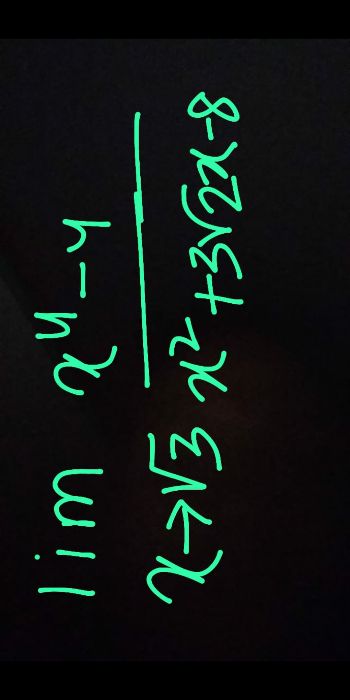
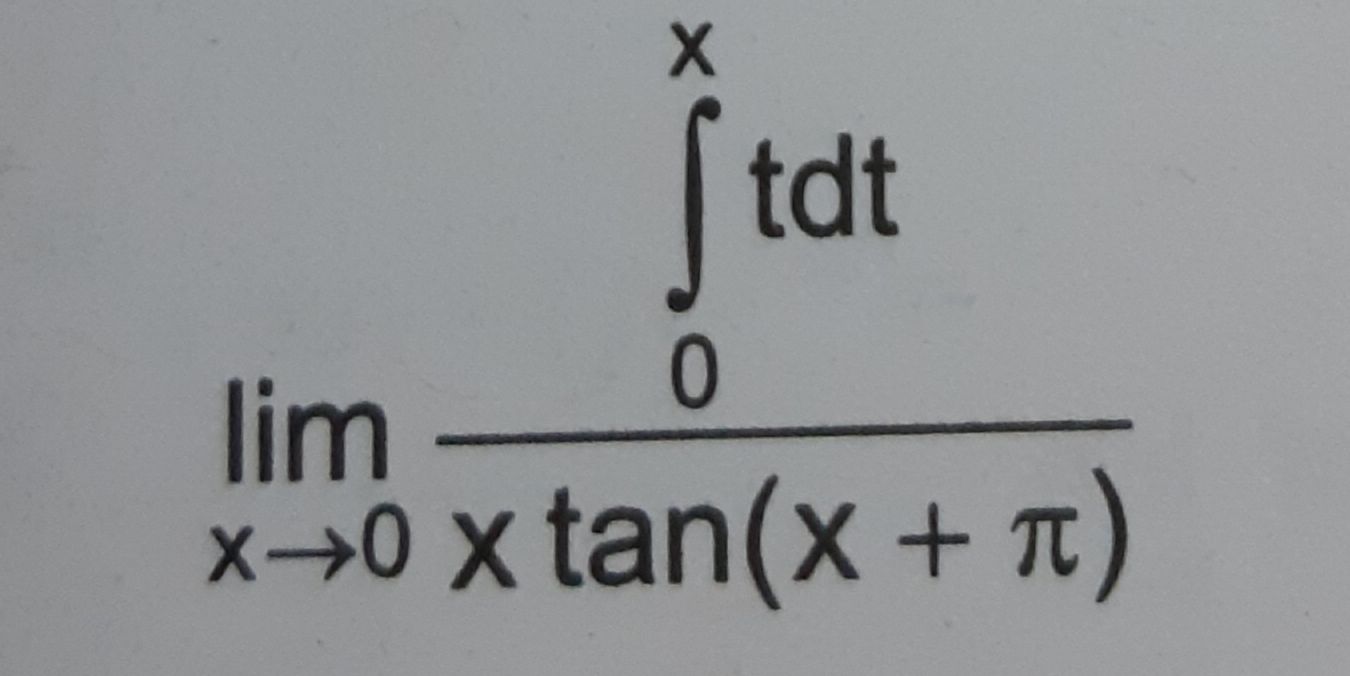
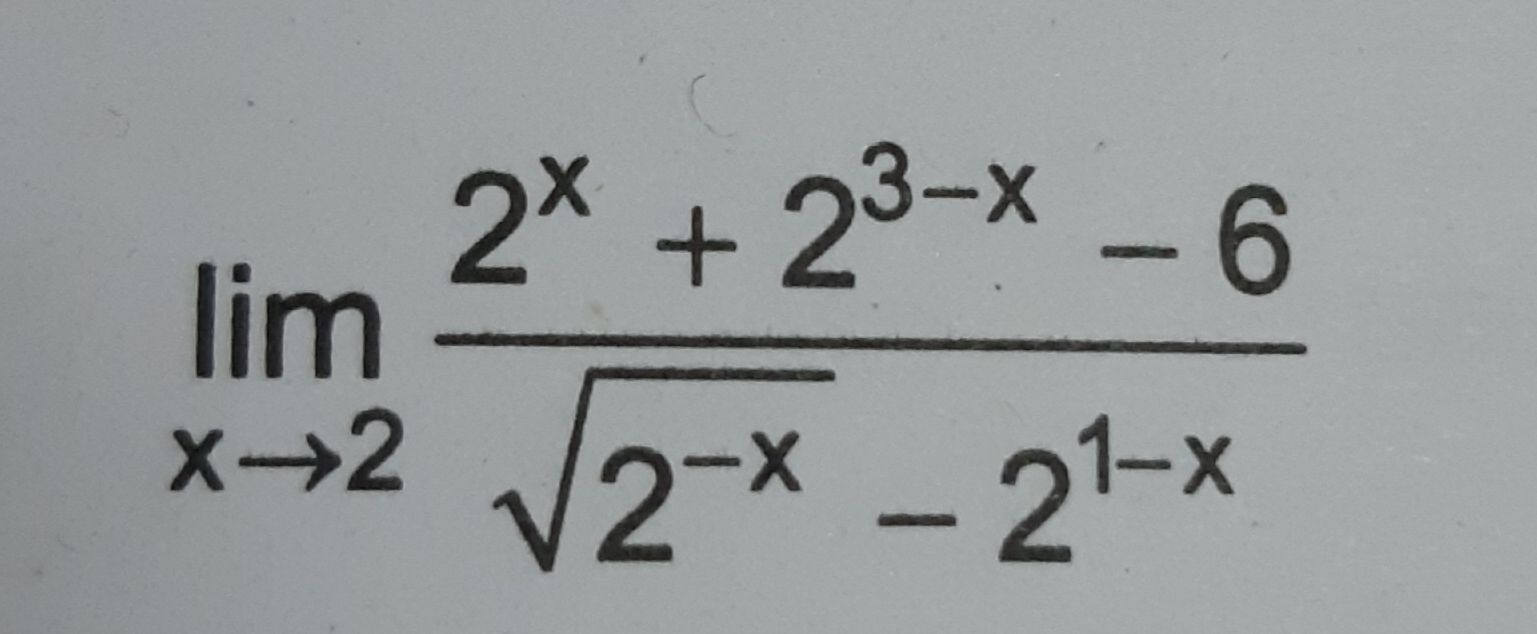
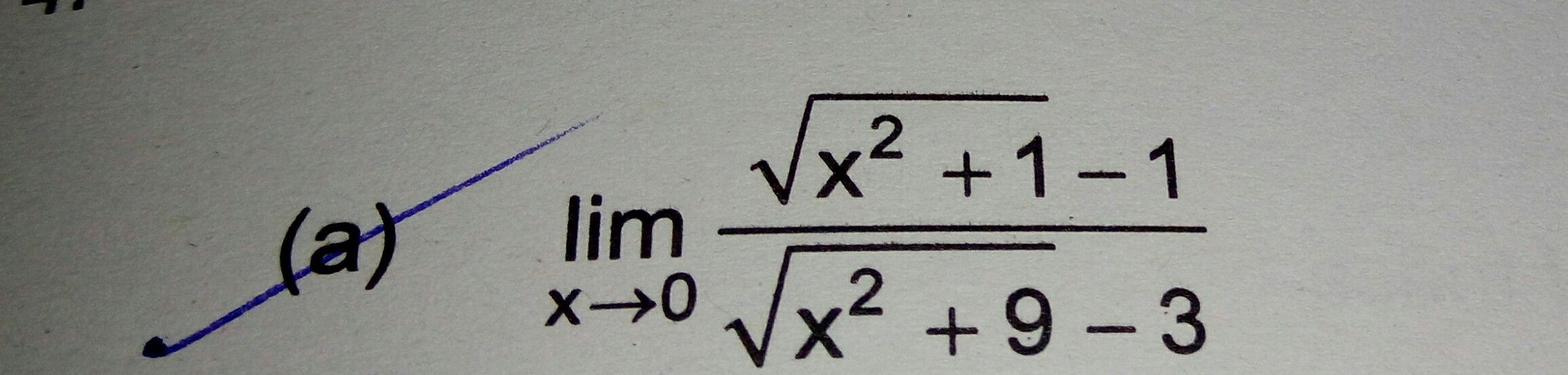
 .find lim f(x) x->1
.find lim f(x) x->1