Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

In a triangle ABC,right angled at B, AC=b, AB=a. A line is drawn from point C to the opposite side AB intersecting it at D such that AD=DB . Determine sin^2 C+ cos^2C.
 
Asked by Jerlin George | 18 Jun, 2015, 11:02: PM
answered-by-expert Expert Answer
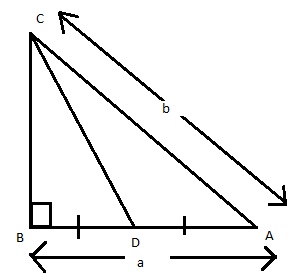
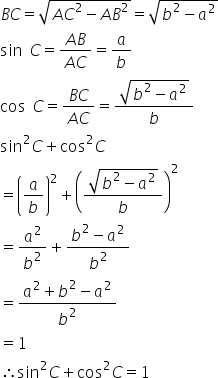
B C equals square root of A C squared minus A B squared end root equals square root of b squared minus a squared end root sin space C equals fraction numerator A B over denominator A C end fraction equals a over b cos space C equals fraction numerator B C over denominator A C end fraction equals fraction numerator square root of b squared minus a squared end root over denominator b end fraction sin squared C plus cos squared C equals open parentheses a over b close parentheses squared plus open parentheses fraction numerator square root of b squared minus a squared end root over denominator b end fraction close parentheses squared equals a squared over b squared plus fraction numerator b squared minus a squared over denominator b squared end fraction equals fraction numerator a squared plus b squared minus a squared over denominator b squared end fraction equals 1 therefore sin squared C plus cos squared C equals 1
Answered by Prasenjit Paul | 19 Jun, 2015, 11:04: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
sinA(1+tanA)+CosA(1+cotA)=seA+cosecA
question image
Asked by pm86982 | 10 Apr, 2023, 12:24: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Sin^2A/2+Sin^2(B+C/2)
Asked by adinaditi29 | 14 Mar, 2022, 12:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove that 1+sina-cosa/1+sina+cosa=√1-cos/√1+cosa
Asked by ambarishpatil7 | 28 Sep, 2021, 08:49: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
sin teta + 2cos teta =1 prove that 2sin teta - cos teta =2
Asked by manish.mayuka | 02 May, 2021, 02:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Cosec²72° - tan²18°=1
Asked by abhishekmonupatel27 | 23 Feb, 2021, 04:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
square root of fraction numerator 1 plus sin empty set over denominator 1 minus sin empty set end fraction end root plus square root of fraction numerator 1 minus sin empty set over denominator 1 plus sin empty set end fraction end root equals 2 s e c empty set
Asked by kushalkush371 | 27 Dec, 2020, 07:31: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Show that … cosec theta minus 2sin cube theta upon 2cos cube theta minus cos theta is equals to tan theta
Asked by pramoddomarp121 | 26 Sep, 2020, 06:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
please help
question image
Asked by satishcharan533 | 24 Sep, 2020, 02:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
please help me to solve this problem
question image
Asked by kalladaprem | 24 Sep, 2020, 08:20: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
how to prive
question image
Asked by farkadeamol9 | 28 Aug, 2020, 10:53: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×