CBSE Class 11-science Answered
I'm unable to understand the 2nd law of kepler please give me some information about this
and send me video which show the 2nd kepler law
please help
I'm new
Asked by kashmirsunil | 24 May, 2020, 21:06: PM
Kepler's second law:
Consider that a planet of mass 'm' revolving around the Sun of mass 'M' in a circular orbit of radius 'r'. Let 'v' be its orbital velocity. Suppose that at any isntant the planet is at point A in its orbit and after an in small time dt, it reaches point B. As such, the circular path of the planet between points A and B may be considered as straight.
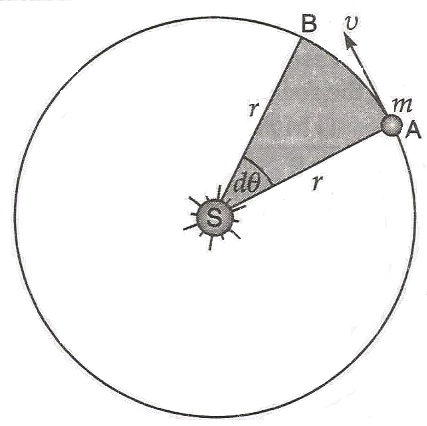 If dA is small area swept by the line joining the planet to the Sun in time dt, then
dA=area of ΔABS=
If dA is small area swept by the line joining the planet to the Sun in time dt, then
dA=area of ΔABS=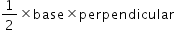 or dA=
or dA=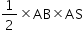 .... (1)
If dθ is the angular displacement of the planet in time dt i.e., when it moves from point A to B, then AB=r dθ.
Substituting AB with rdθ and AS with 'r' in equation(1), we get,
.... (1)
If dθ is the angular displacement of the planet in time dt i.e., when it moves from point A to B, then AB=r dθ.
Substituting AB with rdθ and AS with 'r' in equation(1), we get,
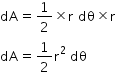 Dividing the above equation by dt, we get,
Dividing the above equation by dt, we get,
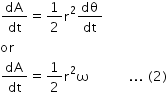 where ω=
where ω=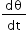 is the angular speed of the planet in its orbit and
is the angular speed of the planet in its orbit and 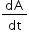 is the areal velocity of the planet.
Multiplying and divind the R.H.S of the equation(2) by 'm' i.e., the mass of the planet, we get,
is the areal velocity of the planet.
Multiplying and divind the R.H.S of the equation(2) by 'm' i.e., the mass of the planet, we get,
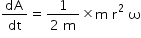 Since, m r2 ω = L, the angular momentum of the planet about the axis through the Sun, we have,
Since, m r2 ω = L, the angular momentum of the planet about the axis through the Sun, we have,
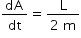 ... (3)
As no external torque acts on the planet during its orbital motion, its angular momentum (L) must remain constant. Since both L amd m are constant, the equation(3) becomes,
... (3)
As no external torque acts on the planet during its orbital motion, its angular momentum (L) must remain constant. Since both L amd m are constant, the equation(3) becomes, 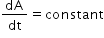 ... (4)
Hence, when a planet moves around the Sun, its areal velocity remains constant. It proves Kepler's second law of planetary motion.
... (4)
Hence, when a planet moves around the Sun, its areal velocity remains constant. It proves Kepler's second law of planetary motion.
For video based explanation click on link given below in blue: - 
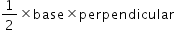
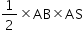 .... (1)
.... (1)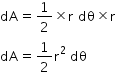
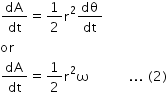
 is the angular speed of the planet in its orbit and
is the angular speed of the planet in its orbit and 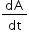 is the areal velocity of the planet.
is the areal velocity of the planet.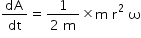
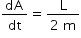 ... (3)
... (3)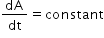 ... (4)
... (4)PS : -You will be required to fill in the details if the pop up comes up asking for the same.
Answered by Shiwani Sawant | 24 May, 2020, 23:02: PM
Concept Videos
CBSE 11-science - Physics
Asked by varma.renu9481 | 17 Mar, 2023, 18:26: PM
CBSE 11-science - Physics
Asked by kashmirsunil | 24 May, 2020, 21:06: PM
CBSE 11-science - Physics
Asked by satishkashyap02022004 | 29 Apr, 2020, 15:07: PM
CBSE 11-science - Physics
Asked by gharesaiprasad1224 | 27 Apr, 2020, 20:40: PM
CBSE 11-science - Physics
Asked by Officialayush1661 | 17 Mar, 2019, 23:18: PM
CBSE 11-science - Physics
Asked by nellore.jayasai | 16 Jan, 2019, 07:58: AM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM