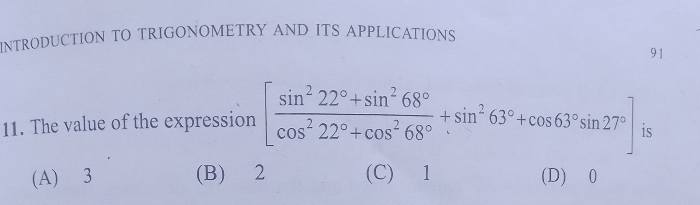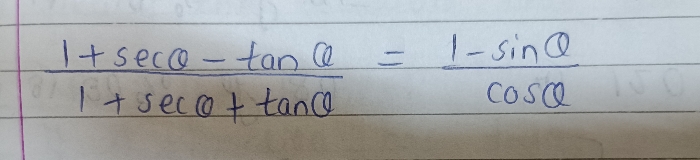CBSE Class 10 Answered
if x = asecA+btanA and y= atanA+bsecA . prove that x^2 - y^2 = a^2 - b^2
Asked by LakshmiSriram | 12 Sep, 2013, 12:46: PM
Given, x = asecA+btanA and y= atanA+bsecA
Now,
LHS = x^2 - y^2
= (asecA+btanA)^2 - (atanA+bsecA)^2
= a^2sec^2A + b^2tan^2A + 2absecAtanA - a^2tan^2A - b^2sec^2A - 2abtanAsecA
= a^2 (sec^2A - tan^2A) + b^2 (tan^2A - sec^2A)
= a^2 (1) + b^2 (-1) (Since, 1+tan^2A = sec^2A)
= a^2 - b^2
= RHS
Answered by | 12 Sep, 2013, 10:28: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by raopaidi | 25 Apr, 2024, 04:06: PM
CBSE 10 - Maths
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by jayashreelatha04 | 17 Mar, 2024, 05:38: PM
CBSE 10 - Maths
Asked by gauravgupta.20008 | 03 Feb, 2024, 05:36: PM
CBSE 10 - Maths
Asked by sathwicksathwick06 | 01 Feb, 2024, 07:30: PM
CBSE 10 - Maths
Asked by tanujmaan58 | 18 Jan, 2024, 08:47: PM