Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

if nsinA=mcosA, PROVE THAT:
(msinA-ncosA/msinA+ncosA) (BOTH R ONE TERM, THEN NEW TERM IS)  + (msinA+ncosA/msinA+ncosA)=2(m to the power 4+ nto the power 4/m to the power4-n to the power 4)
Asked by smruti2002ranjan | 21 Sep, 2016, 11:56: PM
answered-by-expert Expert Answer
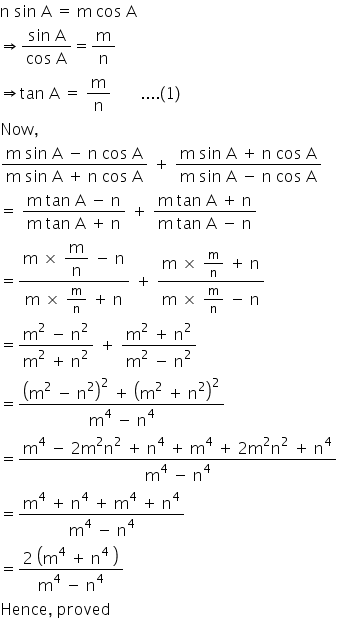
begin mathsize 16px style straight n space sin space straight A space equals space straight m space cos space straight A rightwards double arrow fraction numerator sin space straight A over denominator cos space straight A end fraction equals straight m over straight n rightwards double arrow tan space straight A space equals space straight m over straight n space space space space space space space.... left parenthesis 1 right parenthesis Now comma fraction numerator straight m space sin space straight A space minus space straight n space cos space straight A over denominator straight m space sin space straight A space plus space straight n space cos space straight A end fraction space plus space fraction numerator straight m space sin space straight A space plus space straight n space cos space straight A over denominator straight m space sin space straight A space minus space straight n space cos space straight A end fraction equals space fraction numerator straight m space tan space straight A space minus space straight n over denominator straight m space tan space straight A space plus space straight n end fraction space plus space fraction numerator straight m space tan space straight A space plus space straight n over denominator straight m space tan space straight A space minus space straight n end fraction equals fraction numerator straight m space cross times space begin display style straight m over straight n end style space minus space straight n over denominator straight m space cross times space straight m over straight n space plus space straight n end fraction space plus space fraction numerator straight m space cross times space straight m over straight n space plus space straight n over denominator straight m space cross times space straight m over straight n space minus space straight n end fraction equals fraction numerator straight m squared space minus space straight n squared over denominator straight m squared space plus space straight n squared end fraction space plus space fraction numerator straight m squared space plus space straight n squared over denominator straight m squared space minus space straight n squared end fraction equals fraction numerator open parentheses straight m squared space minus space straight n squared close parentheses squared space plus space open parentheses straight m squared space plus space straight n squared close parentheses squared over denominator straight m to the power of 4 space minus space straight n to the power of 4 end fraction equals fraction numerator straight m to the power of 4 space minus space 2 straight m squared straight n squared space plus space straight n to the power of 4 space plus space straight m to the power of 4 space plus space 2 straight m squared straight n squared space plus space straight n to the power of 4 over denominator straight m to the power of 4 space minus space straight n to the power of 4 end fraction equals fraction numerator straight m to the power of 4 space plus space straight n to the power of 4 space plus space straight m to the power of 4 space plus space straight n to the power of 4 over denominator straight m to the power of 4 space minus space straight n to the power of 4 end fraction equals fraction numerator 2 space open parentheses straight m to the power of 4 space plus space straight n to the power of 4 space close parentheses over denominator straight m to the power of 4 space minus space straight n to the power of 4 end fraction Hence comma space proved end style
Answered by Rashmi Khot | 22 Sep, 2016, 10:46: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
sinA(1+tanA)+CosA(1+cotA)=seA+cosecA
question image
Asked by pm86982 | 10 Apr, 2023, 12:24: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Sin^2A/2+Sin^2(B+C/2)
Asked by adinaditi29 | 14 Mar, 2022, 12:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove that 1+sina-cosa/1+sina+cosa=√1-cos/√1+cosa
Asked by ambarishpatil7 | 28 Sep, 2021, 08:49: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
sin teta + 2cos teta =1 prove that 2sin teta - cos teta =2
Asked by manish.mayuka | 02 May, 2021, 02:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Cosec²72° - tan²18°=1
Asked by abhishekmonupatel27 | 23 Feb, 2021, 04:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
square root of fraction numerator 1 plus sin empty set over denominator 1 minus sin empty set end fraction end root plus square root of fraction numerator 1 minus sin empty set over denominator 1 plus sin empty set end fraction end root equals 2 s e c empty set
Asked by kushalkush371 | 27 Dec, 2020, 07:31: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Show that … cosec theta minus 2sin cube theta upon 2cos cube theta minus cos theta is equals to tan theta
Asked by pramoddomarp121 | 26 Sep, 2020, 06:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
please help
question image
Asked by satishcharan533 | 24 Sep, 2020, 02:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
please help me to solve this problem
question image
Asked by kalladaprem | 24 Sep, 2020, 08:20: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
how to prive
question image
Asked by farkadeamol9 | 28 Aug, 2020, 10:53: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×