CBSE Class 11-science Answered
If A+B+C=pi , then equality of equation
(1/2)(cosA cosB + cosB cosC + cosC cosA)
must hold:
a) <= 3/2. b) >=(-3) c) <=3/8 d) >=(-1)
Asked by shanujam03 | 03 Oct, 2020, 20:59: PM
Given: A+B+C=pi
Consider,
(1/2)(cosA cosB + cosB cosC + cosC cosA)
= (1/4)(2cosA cosB + 2cosB cosC + 2cosC cosA)
= (1/4)[(cosA + cosB + cosC)2 - (cos2A + cos2B + cos2C)]
>= (1/4)[1 - (cos2A + cos2B + cos2C)]
As (cosA + cosB + cosC)2 >= 1
Use this inequality and get the inequality for (1/2)(cosA cosB + cosB cosC + cosC cosA)
Answered by Renu Varma | 06 Oct, 2020, 10:52: AM
Concept Videos
CBSE 11-science - Maths
Asked by bimanmandal53361 | 15 Jan, 2024, 00:32: AM
CBSE 11-science - Maths
Asked by mishraparveen1234 | 15 Jun, 2022, 16:56: PM
CBSE 11-science - Maths
Asked by shanujam03 | 03 Oct, 2020, 20:59: PM
CBSE 11-science - Maths
Asked by richasingh0708.bmps | 23 Jun, 2020, 22:00: PM
CBSE 11-science - Maths
Asked by dppanigrahiadv | 26 May, 2020, 19:03: PM
CBSE 11-science - Maths
Asked by lykanbeast04 | 21 May, 2020, 18:49: PM
CBSE 11-science - Maths
Asked by Singhnitish1475 | 11 May, 2019, 01:46: AM





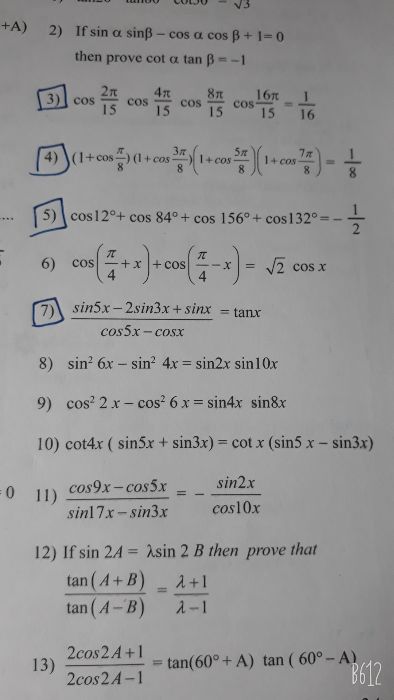
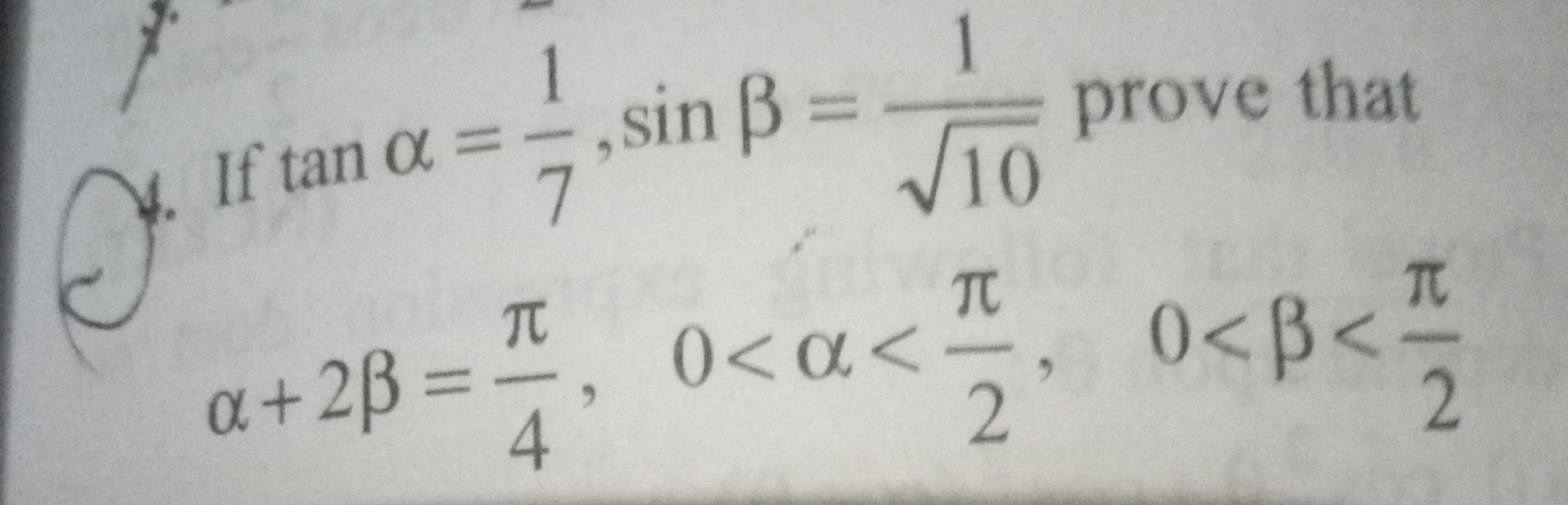
 ,then what is the value of cosec(7
,then what is the value of cosec(7