CBSE Class 10 Answered

If a and b are two positive odd integers prove that one out of a+b÷2 and a-b÷2 is odd and other is even

Asked by shabnakader | 22 Jun, 2017, 06:24: PM

Expert Answer

Given that both a and b are positive odd integers.

Let a = 2j + 1 and b = 2k+ 1, where j and k can be

i) both odd or

ii) both even or

iii) one odd and a > b

Now, if j and k are both odd and both even (cases i and ii) then,

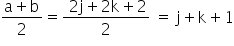
begin mathsize 16px style fraction numerator straight a plus straight b over denominator 2 end fraction equals fraction numerator space 2 straight j plus 2 straight k plus 2 over denominator 2 end fraction space equals space straight j plus straight k plus 1 end style

Now j + k will be always even (sum of two odd number is even and sum of two even numbers is definitely even)

This means j + k + 1 is definitely odd

begin mathsize 16px style rightwards double arrow fraction numerator left parenthesis straight a plus straight b right parenthesis over denominator 2 end fraction end style

is definitely odd

and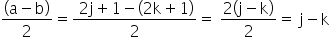

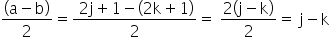
begin mathsize 16px style fraction numerator left parenthesis straight a minus straight b right parenthesis over denominator 2 end fraction equals fraction numerator space 2 straight j plus 1 minus left parenthesis 2 straight k plus 1 right parenthesis over denominator 2 end fraction equals space fraction numerator 2 left parenthesis straight j minus straight k right parenthesis over denominator 2 end fraction equals space straight j minus straight k end style

which will always be even since the difference of odd as well as even numbers is even.

Hence, j - k is definitely even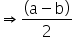

begin mathsize 16px style rightwards double arrow fraction numerator left parenthesis straight a minus straight b right parenthesis over denominator 2 end fraction end style

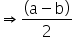is definitely even.

Now for case (iii) lets say j is odd and k is even

begin mathsize 16px style rightwards double arrow fraction numerator left parenthesis straight a plus straight b right parenthesis over denominator 2 end fraction equals space fraction numerator left parenthesis 2 straight j plus 2 straight k plus 2 right parenthesis over denominator 2 end fraction equals space straight j plus straight k plus 1. end style

Now j + k will be always odd (sum of one odd and one even number is always odd )

This means j + k + 1 is definitely even

begin mathsize 16px style rightwards double arrow fraction numerator left parenthesis straight a plus straight b right parenthesis over denominator 2 end fraction end style

is definitely even.

similar logic goes for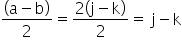

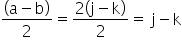begin mathsize 16px style fraction numerator left parenthesis straight a minus straight b right parenthesis over denominator 2 end fraction equals fraction numerator 2 left parenthesis straight j minus straight k right parenthesis over denominator 2 end fraction equals space straight j minus straight k end style

which will definitely be odd.

Hence proved.

Answered by Rebecca | 22 Jun, 2017, 07:22: PM

Application Videos