CBSE Class 10 Answered

Let ABCD be a square and let A(5, 4) and C(1, -6) be the given two vertices.

Also, let (x, y) be the coordinates of point B. 
Since AB=BC

(AB)² = (BC)²

(x - 5)² + (y - 4)² = ­­(1 - x)² + (-6 - y)²

Or x² -10x + 25 + y² - 8y + 16 = 1 + x² - 2x + 36 + 12y + y²

-10x + 25 - 8y + 16 = 1 - 2x + 36 + 12y

-8x - 20y = 37 - 41

-4(2x + 5y) = -4

2x + 5y = 1    ....(1)

In right angled triangle ABC,

AB² + BC² = AC²

(x - 5)² + (y - 4)² + (x - 1)² + (y + 6)² = (5 - 1)² + (4 + 6)²

x² - 10x + 25 + y² - 8y + 16 + x² - 2x + 1 + y² + 12y + 36 = 16 + 100

2x² + 2y² - 12x + 4y + 78 - 116 = 0

x² + y² - 6x + 2y + 39 - 58 = 0

x² + y² - 6x + 2y - 19 = 0 (ii)

From (i) x = 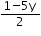 , putting in (ii), we get,

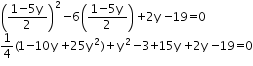
25y² - 10y + 1 + 4y² + 68y - 88 = 0

29y² + 58y - 87 = 0

 y² + 2y - 3 = 0

(y + 3)(y - 1) = 0

    y = -3, 1

When y = -3, x = 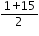= 8 ;

when y = 1, x =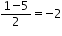 

Therefore, required points are (-2, 1), (8, -3)