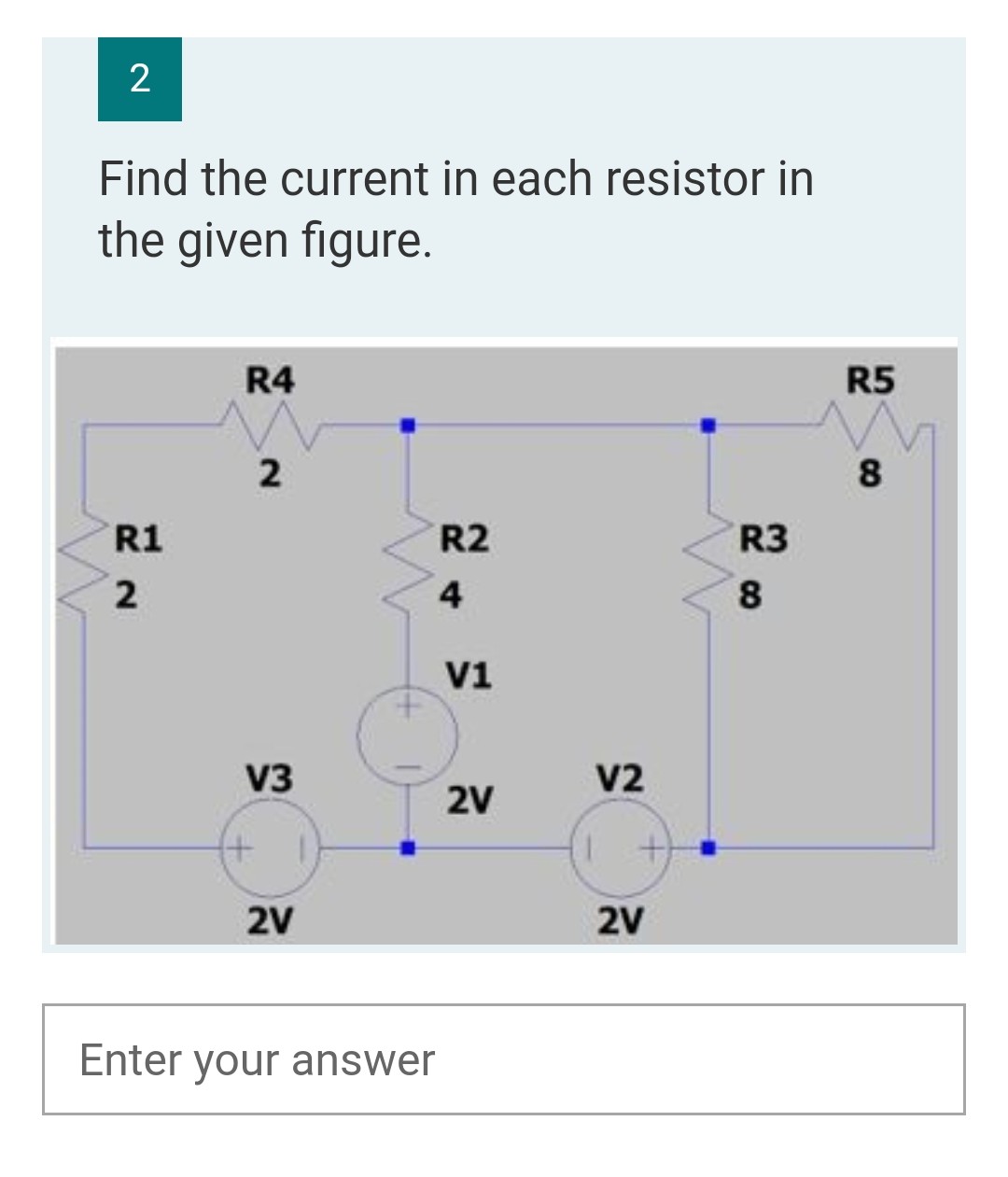
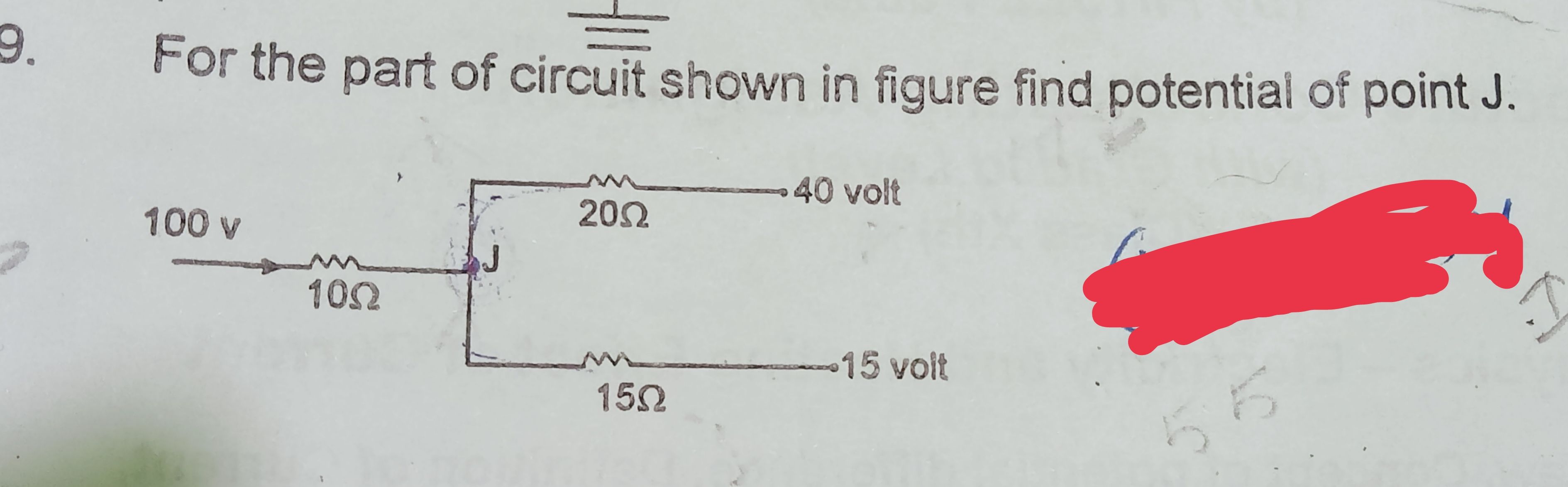CBSE Class 12-science Answered
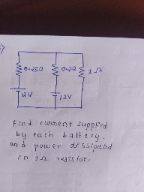
find the voltage across each resistor using kirchhoff rules
Asked by carthi66 | 11 Nov, 2021, 14:49: PM
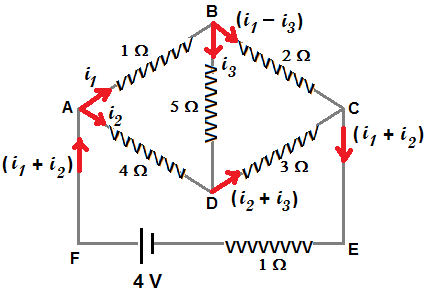
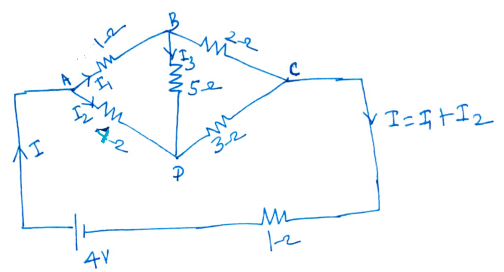
Current distribution in the circuit is assumed as shown in figure.
If we apply Kirchoff's voltage law to the closed loop ADCEFA , we get the following equation
4 i2 + 3 ( i2 + i3 ) + ( i1 + i2 ) = 4 ..............................(1)
If we apply Kirchoff's voltage law to the closed loop ABCEFA , we get the following equation
i1 + 2 ( i1 - i3 ) + ( i1 + i2 ) = 4 ..............................(2)
By subtracting eqn.(2) from eqn.(1) , we get
7 i2 - 3 i1 + 5 i3 = 0 or 7 i2 + 5 i3 = 3 i1 ......................... (3)
If we apply Kirchoff's voltage law to the closed loop BDCB , we get the following equation
5 i3 + 3 ( i2 + i3 ) + 2 ( i1 - i3 ) = 0
By simplifying above expression we get , 3 i2 + 10 i3 = 2 i1 ......................(4)
By solving eqn.(3) and (4) , we get i2 = (4/11) i1 and i3 = (1/11) i1
By substituting i2 and i3 in eqn.(1) , we get i1 = (22/23) A
Hence i2 = (4/11) × (22/23) A = ( 8 / 23 ) A and i3 = ( 1/11) × (22/23) A = ( 2 / 23 ) A
Voltage drop across 1Ω resistor between A and B = 1 × ( 22/23) = (22 / 23 ) V = 0.956 V
Voltage drop across 2Ω resistor between B and C = 2 × [ ( 22/23) - (2/23) ] = (40 / 23 ) V = 1.739 V
Voltage drop across 3Ω resistor between D and C = 3 × [ ( 8/23) + (2/23) ] = (30 / 23 ) V = 1.304 V
Voltage drop across 4Ω resistor between A and D = 4 × (8/23) ] = (32 / 23 ) V = 1.391 V
Voltage drop across 5Ω resistor between B and D = 5 × (2/23) = (10 / 23 ) V = 0.435 V
Voltage drop across 1Ω resistor between E and F = 1 × [ ( 22/23) + (8/23) ] = (30 / 23 ) V = 1.304 V
Answered by Thiyagarajan K | 12 Nov, 2021, 00:26: AM
Concept Videos
CBSE 12-science - Physics
Asked by mailtoanjalip2005 | 16 Mar, 2024, 20:22: PM
CBSE 12-science - Physics
Asked by nikhilsai2616 | 19 Nov, 2023, 01:05: AM
CBSE 12-science - Physics
Asked by snehashiragannavar773 | 21 Oct, 2023, 14:38: PM
CBSE 12-science - Physics
Asked by komalbrar0987 | 17 May, 2023, 18:15: PM
CBSE 12-science - Physics
Asked by nudratnigar | 10 May, 2022, 12:02: PM
CBSE 12-science - Physics
Asked by divyabharti14042004 | 18 Jan, 2022, 14:52: PM
CBSE 12-science - Physics
Asked by carthi66 | 11 Nov, 2021, 14:49: PM
CBSE 12-science - Physics
Asked by umeshts142 | 13 Oct, 2021, 08:14: AM
CBSE 12-science - Physics
Asked by najeeb.razvi | 09 Aug, 2021, 18:45: PM