CBSE Class 11-science Answered
Find the equation of the parabola with vertex [2,-3] and focus [0,5]
Asked by arkabanerjee | 29 Jan, 2011, 09:05: PM
Dear student,
Let A(2, -3) be the vertex and F(0, 5) be the focus.
Let the axis meet the directrix at a point Z(α,β).
Then, A is the mid point of ZF.
So, 2 = α+0/2
α=4
and, -3=β+5/2
β=-11
Thus, the coordinates of Z are (4, -11).
Now, slope of ZF = 5+11/0-4=-4
So, slope of the directrix = 1/4
Thus, the directrix is a line passing through the point (4, -11) and has a slope equal to 1/4.
Thus, the equation of the directrix is given by:
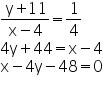
Let P (x, y) be any point on the parabola. Then,
PF = length of the perpendicular from P on x-4y-48=0
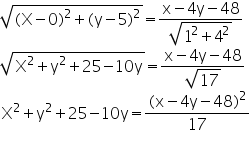
Simplify this expression to get the required equation of the parabola.
We hope that this clarifies your query.
Regards,
Team
TopperLearning
Answered by | 07 Feb, 2011, 09:46: PM
Concept Videos
CBSE 11-science - Maths
Asked by praveenaditya843 | 22 Dec, 2023, 10:41: AM
CBSE 11-science - Maths
Asked by praveenaditya843 | 21 Dec, 2023, 07:39: PM
CBSE 11-science - Maths
Asked by shakyajayprakash2006 | 08 Jun, 2022, 05:26: PM
CBSE 11-science - Maths
Asked by sbipo2000 | 23 Feb, 2020, 03:43: PM
CBSE 11-science - Maths
Asked by kandappan | 08 Feb, 2020, 11:29: AM
CBSE 11-science - Maths
Asked by Tejravi969 | 19 Aug, 2019, 06:08: AM
CBSE 11-science - Maths
Asked by Praktu111 | 09 Jun, 2019, 08:18: AM
CBSE 11-science - Maths
Asked by rushabh1234 | 23 Jan, 2019, 08:59: PM











