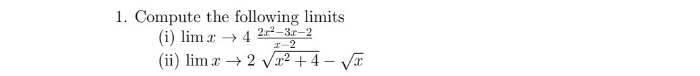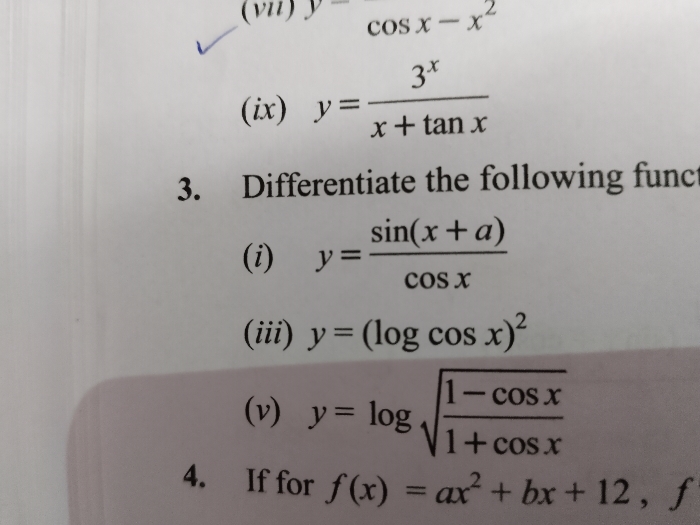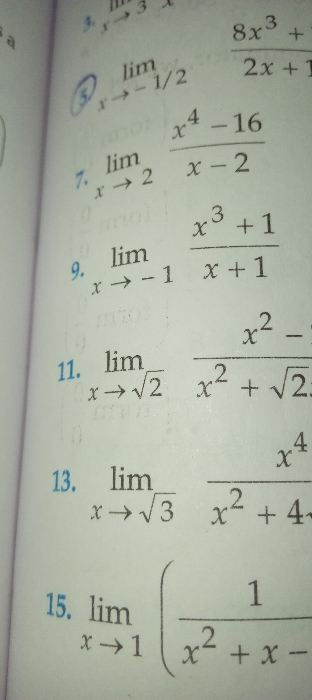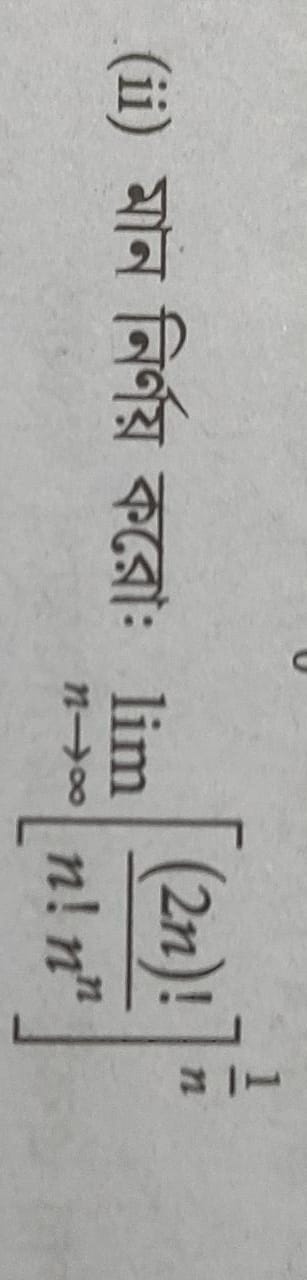CBSE Class 11-science Answered
find the derivate of x raise to n from first principle?
Asked by raghavirao12 | 21 Nov, 2014, 09:36: PM

Answered by Vimala Ramamurthy | 22 Nov, 2014, 08:14: AM
Concept Videos
CBSE 11-science - Maths
Asked by kanishkatutejasirsa | 09 Mar, 2024, 11:08: AM
CBSE 11-science - Maths
Asked by ns091764623 | 03 Mar, 2024, 08:33: AM
CBSE 11-science - Maths
Asked by pndash1974 | 08 Nov, 2023, 08:40: PM
CBSE 11-science - Maths
Asked by amisharanjan14 | 30 Sep, 2023, 07:28: PM
CBSE 11-science - Maths
Asked by sdmbotch1123 | 18 Jan, 2023, 11:02: PM
CBSE 11-science - Maths
Asked by kushik.jnp2025 | 15 Jan, 2023, 12:00: AM
CBSE 11-science - Maths
Asked by ankitkanjilal409 | 30 Dec, 2022, 08:25: PM
CBSE 11-science - Maths
Asked by huzaifashangroo | 28 Dec, 2022, 06:57: PM