JEE Class main Answered

Find equivalent resistance

Asked by ojastej235 | 29 Sep, 2021, 19:56: PM

Expert Answer

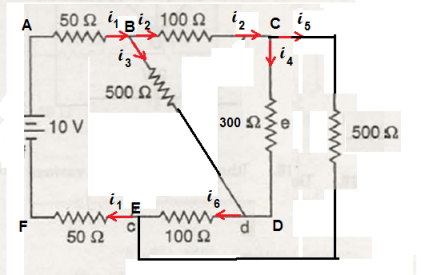
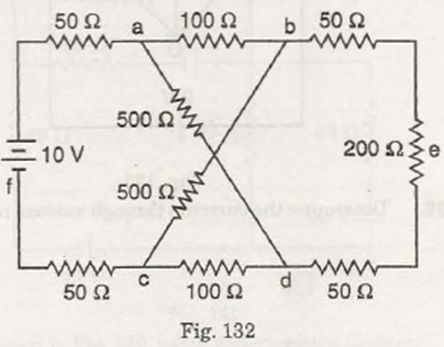
It is assumed equivalent resistance across battery is to be determined.

If we see the given circuit , we have 50 Ω resistors are connected at both side of 200 Ω resistor ( near point marked as e in given circuit ) .

Hence the series combination of 50 Ω, 200 Ω and 50 Ω is replaced by a 300 Ω resistance .

500 Ω resistance connected between b and c is redrawn as shown in above figure .

Let us assume current distribution as shown in figure.

If we apply Kirchoff's voltage law to the closed loop ABDEF , we get

50 i₁ + 500 i₃ + 100 i₆ + 50 i₁ = 10 .........................(1)

At node D , i₆ = i₃ + i₄ ..........................(2)

Using eqn.(2) , we rewrite eqn.(1) as , 100 i₁ + 600 i₃ + 100 i₄ = 10 ............................ (3)

If we apply Kirchoff's voltage law to the closed loop BCDB , we get

100 i₂ + 300 i₄ - 500 i₃ = 0 ..................................(4)

At node B , we have , i₁ = i₂ + i₃ ...........................(5)

Using eqn.(5) , we rewrite eqn.(3) as , 100 i₂ + 700 i₃ + 100 i₄ = 10 ........................... (6)

By subtracting eqn.(4) from eqn.(6) , we get , 1200 i₃ - 200 i₄ = 10 .............................(7)

If we apply Kirchoff's voltage law to the closed loop CEDC , we get

500 i₅ - 100 i₆ - 300 i₄ = 0 .......................... (8)

at Node C , i₅ = i₂ - i₄ .......................(9)

By using eqn.(2) and eqn.(9) , we rewrite eqn.(8) as

500 i₂ - 100 i₃ - 900 i₄ = 0 ......................(10)

By multiplying eqn.(4) by 5 and subtracting from eqn.(8) ,

we get , i₃ = i₄ ...................(11)

Using eqn.(11) , we get i₃ from eqn.(7) as i₃ = ( 1/100 ) A

Hence we have , i₃ = i₄ = ( 1/100 ) A

Using values of i₃ and i₄ in eqn.(10) , we get i₂ = 2/100 A

Hence , i₁ = i₂ + i₃= (1/100) +(2/100) A = (3/100) A

Since current drawn from battery is i₁ = (3/100) A ,

Equivalent resistance = Voltage /current = 10 / (3/100) = 333.33 Ω

Answered by Thiyagarajan K | 29 Sep, 2021, 23:33: PM

Concept Videos