CBSE Class 11-science Answered
eg. v = 2x ; assume t = 0 ; x = 2 m ; find a(t)?
Asked by kapilkulhari | 23 May, 2019, 06:56: PM
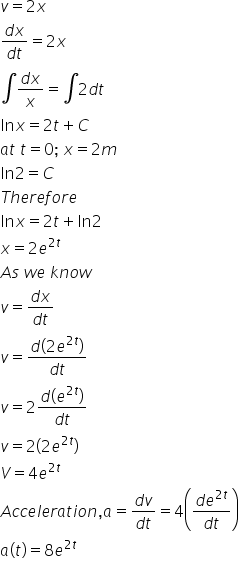
Answered by Utkarsh Lokhande | 24 May, 2019, 11:33: AM