CBSE Class 9 Answered
Can you please provide at least 2 questions each along with solutions of Graphical derivation of the following equations of motion.
1) To Derive v = u + at by Graphical Method
2) To Derive s = ut + ½at² by Graphical Method
3) To Derive v² = u² + 2as by Graphical Method
Also, please provide some links to similar questions and solutions in the Topperlearnings online knowledgebase.
Thanks in advance for your early reply.
Asked by nayonika.online.learning | 06 May, 2018, 14:33: PM
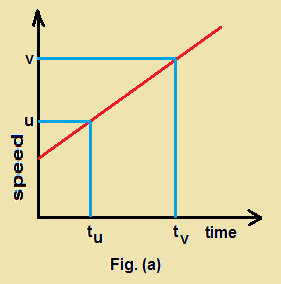
Let an object is subjected to uniform acceleration so that its speed keep on increasing at uniform rate. Fig.(a) shows the graph for its motion.
Acceleration = rate of change of speed = change in speed / time
As shown in figure let u be the speed at time tu and v be the spped at time tv
change in speed in time interval (tv-tu) = v-u
acceleration a = (v-u)/(tv-tu)
let us denot (tv-tu) = t; then acceleration a = (v-u)/t ; v = u+at
-----------------------------------------------------------------------------------
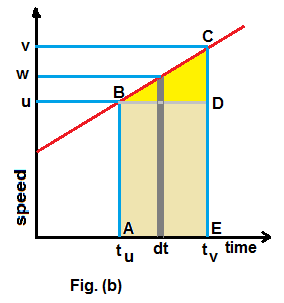
Fig.(b) shows the graphical representation of an object which is subjected to uniform acceleration so that its speed increasing at uniform rate.
Basically the distance travelled in a time t is product of speed and time.
Since the speed is keep on increasing, the distance travelled beteen the time tv and time tu is the area under the segment BC of line graph,
i.e. area of quadilateral ABCDE. This can be seen from figure, if the area is divided into a small time interval dt at the time when the speed is w and
the displacement is w×dt. Like that displacements are calculated at different small interval throughout the region and added together.
Hence finally we get area of region ABCDE. The quadilateral ABCDE is divided into two area, i.e. rectangle ABDE and Triangle BCD.
Area of ABCDE = area of ABDE + area of BCD = AB×AE + (1/2)×BD×CD = u×(tv-tu)+(1/2)(tv-tu)(v-u)
let us denote (tv-tu) = t and also substitue (v-u) = a×t , where a is acceleration
hence we get Area of ABCDE = S = u×t + (1/2)a×t2 , where S is the distance travelled between time tv and tu
There is an alternate way of calculating the area ABCDE. This area ABCDE can be viewed as a trapezeium with parallelsides AB and CE.
Area of trapezeium = (1/2)(AB+CE)×AE = (1/2)(u+v)(tv-tu) = (1/2)(u+v)×t
let us substitute t = (v-u)/a using the previous relation v = u+at in the above equation.
Area of trapezeium = S = (1/2)×(v+u)×(v-u)/a ; we get v2 = u2+2aS
Answered by Thiyagarajan K | 06 May, 2018, 17:18: PM
Application Videos
Concept Videos
CBSE 9 - Physics
Asked by nsandhyabati | 11 Jul, 2024, 21:41: PM
CBSE 9 - Physics
Asked by mintinmaurya | 25 Jun, 2024, 15:03: PM
CBSE 9 - Physics
Asked by kamakshi.tulasi | 10 Jun, 2024, 09:59: AM
CBSE 9 - Physics
Asked by nittavijayalaxmigayatri | 08 Jun, 2024, 12:36: PM
CBSE 9 - Physics
Asked by varshuparekh | 03 Jun, 2024, 18:34: PM
CBSE 9 - Physics
Asked by ashishtyagi642 | 17 May, 2024, 06:34: AM
CBSE 9 - Physics
Asked by mailtoparvathyprajith | 08 Feb, 2024, 18:45: PM
CBSE 9 - Physics
Asked by mailtoparvathyprajith | 08 Feb, 2024, 12:32: PM
CBSE 9 - Physics
Asked by mailtoparvathyprajith | 08 Feb, 2024, 12:13: PM
CBSE 9 - Physics
Asked by mailtoparvathyprajith | 06 Feb, 2024, 21:50: PM