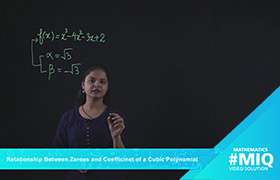CBSE Class 10 Answered

Yes, long division method can be used to find the zeroes of a polynomial. First, we have to find one of the zero of the polynomial by hit and trial method. That zero can be found by looking at the factors of the constant term and their negatives.

Let us find the zeroes of the polynomial p(x) = x³ – 8x² + 9x + 18

Here the factors of 18 are 1, 2, 3, 6, 9.

Now, p(1) = 1 - 8 + 9 + 18, which is not equal to 0.

So, 1 is not a factor of p(x).

Now, consider -1.

p(-1) = 0

Hence, (x + 1) is a factor of p(x).

Now, using long division, divide p(x) by (x + 1). You will get the remainder as 0 and the quotient as (x² - 9x + 18).

This factor can now be factorised as (x - 3)(x - 6).

Thus p(x) = (x + 1)(x - 3)(x - 6)

Hence, the zeroes of p(x) are -1, 3, 6.