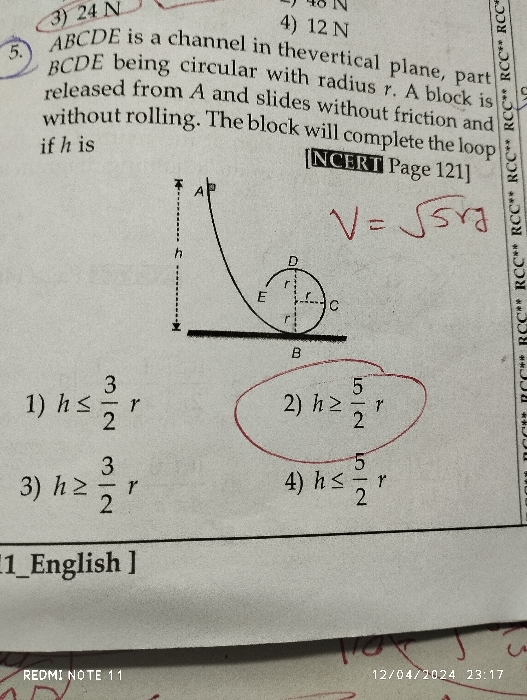NEET Class neet Answered

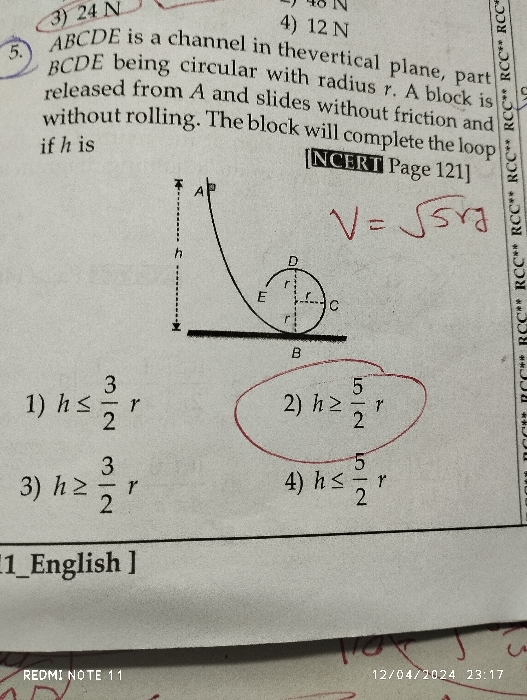
when the block is at the top point D of loop , we have

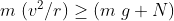
First term in RHS of above expression is weight " mg " and N is normal force .

LHS of above expression is centripetal force required for circular motion .

v is speed of block at D and r is radius of loop .

Minimum speed v is determined by equating normal force N = 0 .

hence we get ,

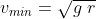
Hence total mechanical energy of block at D

( Kinetic energy + potential energy) ≥ [ (1/2) m v_min²  ] + [ m g (2r) ]

total mechanical energy of block at D ≥  [ (1/2) m g r] + [ m g (2r) ]

total mechanical energy of block at D ≥  [ m g (5/2) r ]

At the point A, where the block is released , by conservation of energy,

total mechanical energy ≥  [ m g (5/2) r ]

At the point A, total mechanical energy is only due to potential energy , we get

m g h ≥  [ m g (5/2) r ]  or   

h  ≥  (5/2) r