CBSE Class 11-science Answered

A tunnel is dug along the diameter of the earth. There is a particle of mass m at the centre of the tunnel. Find the minimum velocity given to the particle so that is just reaches to the surface of the earth (R=radius of the earth)

Asked by akkamal03 | 26 May, 2020, 12:11: PM

Expert Answer

Here we are required to find, minimum velocity given to the particle so that is just reaches to the surface of the earth

Hence, by applying law of conservation of energy,

Initial Total energy of particle = Final energy of particle

Initially the energy of the particle at the centre of the Earth is given as,

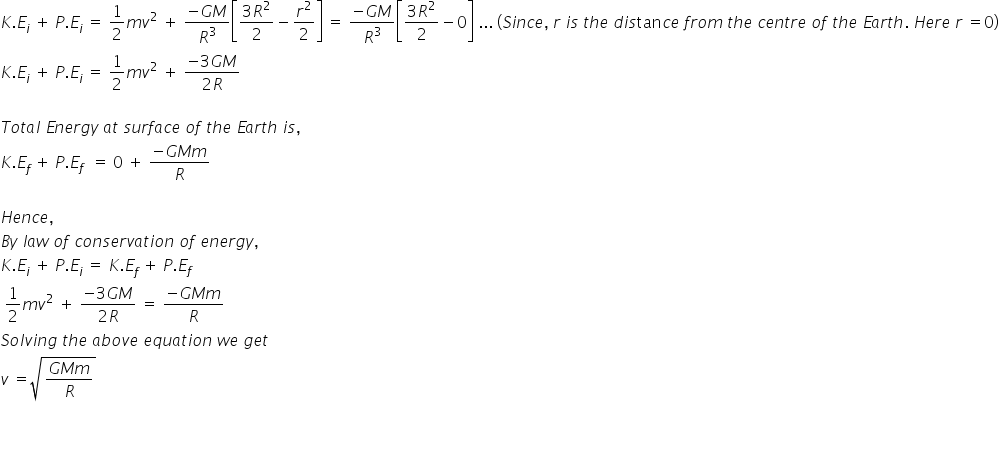
K. E subscript i space plus thin space P. E subscript i space equals space 1 half m v squared space plus space fraction numerator negative G M over denominator R cubed end fraction open square brackets fraction numerator 3 R squared over denominator 2 end fraction minus r squared over 2 close square brackets space equals space fraction numerator negative G M over denominator R cubed end fraction open square brackets fraction numerator 3 R squared over denominator 2 end fraction minus 0 close square brackets space... space left parenthesis S i n c e comma space r space i s space t h e space d i s tan c e space f r o m space t h e space c e n t r e space o f space t h e space E a r t h. space H e r e space r space equals 0 right parenthesis K. E subscript i space plus thin space P. E subscript i space equals space 1 half m v squared space plus space fraction numerator negative 3 G M over denominator 2 R end fraction space T o t a l space E n e r g y space a t space s u r f a c e space o f space t h e space E a r t h space i s comma space K. E subscript f space end subscript plus thin space P. E subscript f space space equals space 0 space plus space fraction numerator negative G M m over denominator R end fraction space H e n c e comma space B y space l a w space o f space c o n s e r v a t i o n space o f space e n e r g y comma space K. E subscript i space plus thin space P. E subscript i space equals space K. E subscript f space end subscript plus thin space P. E subscript f space 1 half m v squared space plus space fraction numerator negative 3 G M over denominator 2 R end fraction space equals space fraction numerator negative G M m over denominator R end fraction S o l v i n g space t h e space a b o v e space e q u a t i o n space w e space g e t v space equals square root of fraction numerator G M m over denominator R end fraction end root space

Answered by Shiwani Sawant | 26 May, 2020, 07:05: PM

Concept Videos

Potential Energy

This video explains the gravitational potential energy and finding out the ...
Gravitational Potential Energy - Part 1

This video explains the universal law of gravitation and the gravitational ...
Conservation of Total Mechanical Energy

This video explains the derivation of the principle of conservation of tota...
Gravitational Potential Energy - Part 2

This video explains the gravitational potential energy and the escape speed...
Potential Energy and Mechanical Energy - Exam Decoded

This video contains practice questions on potential energy and the conserva...

Practice Test

Webinar

Pre Board Assessment

Answered Unanswered My Questions My Answers

CBSE 11-science - Physics

Asked by akkamal03 | 26 May, 2020, 12:11: PM

ANSWERED BY EXPERT

CBSE 11-science - Physics

If R is the radius of earth,then find the energy required to move a body of mass m from an orbit of radius 2R to 3R.

Asked by prabal | 10 Jan, 2019, 09:13: PM

ANSWERED BY EXPERT

CBSE 11-science - Physics

Three masses, each of 1 kg, are placed on the vertices of equilateral triangle of side of length 0.4m.What is the total gravitational potential energy of the configuration?

Asked by prabal | 10 Jan, 2019, 09:10: PM

ANSWERED BY EXPERT

CBSE 11-science - Physics

If the radius of a planet is doubled than of earth with same average densities. What is the ratio there escape velocities.