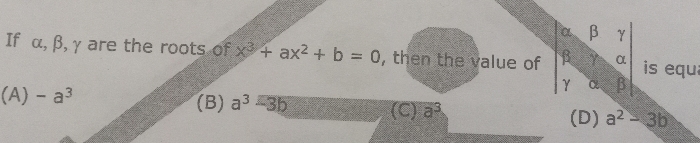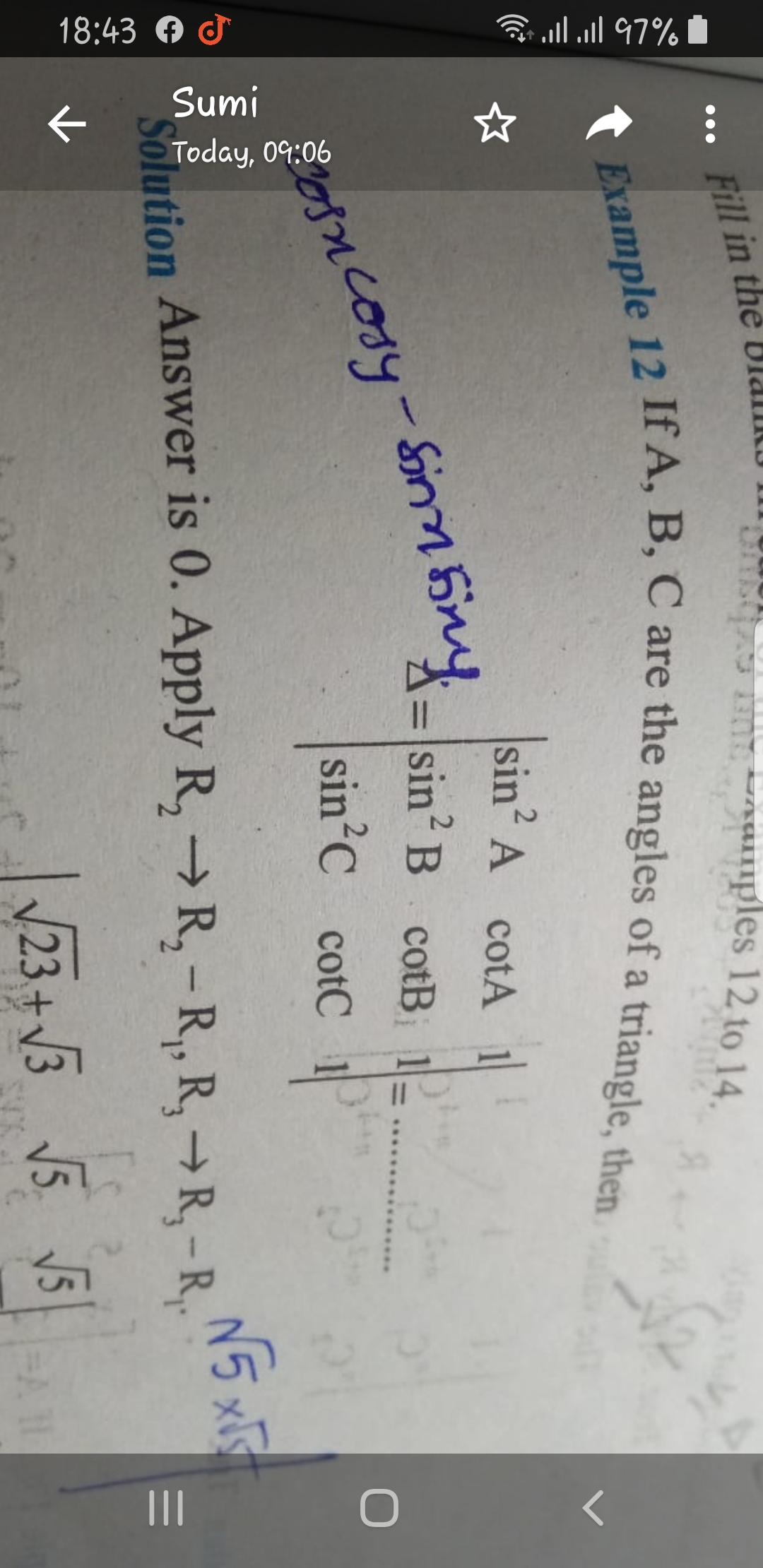CBSE Class 12-science Answered
A square matrix of order 3 has |A|=6 , find |A.adjA|
Asked by mittalishita2002 | 23 Jan, 2020, 08:11: PM
Expert Answer
A square matrix of order 3 has |A|=6 .
|adjA| =|A|n-1 = |A|3-1 =|A|2 = 62 = 36
|A.adjA| = |A||adjA| = 6 × 36 = 216
Answered by Yasmeen Khan | 24 Jan, 2020, 10:47: AM
CBSE 12-science - Maths
Asked by ars22734957 | 13 Mar, 2022, 08:56: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by sushilkumar30122000 | 18 May, 2021, 03:19: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by onkardabhade62 | 30 Dec, 2020, 12:04: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by majethiyarishat9566.12sdatl | 04 May, 2020, 05:26: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by 2003.m.harsh | 24 Apr, 2020, 12:29: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by mittalishita2002 | 23 Jan, 2020, 08:11: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by jain.pradeep | 02 Nov, 2019, 08:16: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by lekhakarthikeyan | 27 Dec, 2018, 02:26: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by lekhakarthikeyan | 01 Apr, 2018, 10:43: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT