A particle of mass m is given speed u at angle theta at topmost point It breaks into two equal parts one comes to rest  find point of landing of second mass

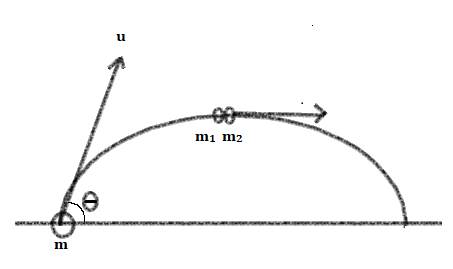
Let's consider that the horizonatl range of particle from where it is projected is R. 

At highest point the horizontal velocity before splitting is = ucosθ

By law of conservation of linear momentum, 

mucosθ = m/2(v)+m/2(0)

Thus, v = 2ucosθ 

As velocity becomes twice the initial velocity range will also become twice and time will depend only on vertical component of velocity. 

Thus, 

The point of landing of other particle = horizontal distance travelled by particle after breaking into two parts 

d = R/2 + R = 3R/2