CBSE Class 11-science Answered
A diwali rocket moves vertically with constant acceleration of 5 ms–2. After some time its fuel exhausted and then it falls freely. If maximum height attained by the rocket is 60m. Then find its speeds when the fuel is just exhausted. (g = 10ms–2)
Asked by aditvk27 | 21 Aug, 2021, 09:56: AM
Let h be the vertical distance travelled by rocket before exhausting the fuel.
Speed v of rocket after moved by a vertical distance h is determined from the following equation of motion
" v = u2 + ( 2 a S ) " ...........................(1)
where u = 0 is initial speed because rocket starts from rest, a = 5 m/s2 is acceleration
and S = h is distance travelled.
v2 = 2 × 5 × h or v =  m/s
m/s
 m/s
m/sIf total vertical distance travelled by rocket is 60 m , distance travelled vertically in gravitational field is (60-h) m .
When the rocket reaches maximum height , its final speed v = 0 . Hence in equation of motion (1) ,
if we substitute v = 0 and initial speed after exhausting fuel u =  m/s , acceleration a = -g = -10 m/s2
m/s , acceleration a = -g = -10 m/s2
 m/s , acceleration a = -g = -10 m/s2
m/s , acceleration a = -g = -10 m/s2 and S = (60-h) m , then we get
10 h = 2 × 10 × (60-h)
we get h = 40 m from above expression
hence speed of rocket immediately after exhausting fuel , v = 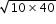 = 20 m/s
= 20 m/s
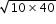 = 20 m/s
= 20 m/s
Answered by Thiyagarajan K | 21 Aug, 2021, 13:14: PM
Concept Videos
CBSE 11-science - Physics
Asked by sulthanxx | 08 Jul, 2024, 19:29: PM
CBSE 11-science - Physics
Asked by tkanmani022 | 11 Jun, 2024, 20:50: PM
CBSE 11-science - Physics
Asked by annpurnasharma1010 | 19 May, 2024, 21:57: PM
CBSE 11-science - Physics
Asked by rajeshabirami27 | 07 May, 2024, 16:31: PM
CBSE 11-science - Physics
Asked by yatin1043 | 06 May, 2024, 14:47: PM
CBSE 11-science - Physics
Asked by om636694 | 04 Mar, 2024, 21:10: PM
CBSE 11-science - Physics
Asked by dhanapolla | 28 Jan, 2024, 10:40: AM
CBSE 11-science - Physics
Asked by santoshyadav6673633 | 26 Jan, 2024, 16:55: PM
CBSE 11-science - Physics
Asked by klvnsnthl | 25 Dec, 2023, 19:50: PM
CBSE 11-science - Physics
Asked by neerajchaurasiya651 | 10 Dec, 2023, 21:32: PM






