Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

1/1.3+1/2.5 +......+1/n(2n+1)
Asked by kien44123986 | 03 Mar, 2020, 08:33: AM
answered-by-expert Expert Answer
To find the sum of the series 1, 1/1.3, 1/2.5, 1/3.7, ... 1/n(2n+1)
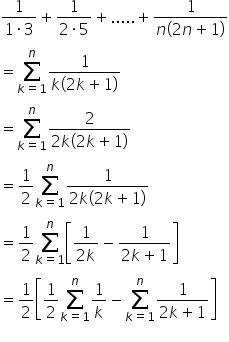
fraction numerator 1 over denominator 1 times 3 end fraction plus fraction numerator 1 over denominator 2 times 5 end fraction plus..... plus fraction numerator 1 over denominator n open parentheses 2 n plus 1 close parentheses end fraction equals sum from k equals 1 to n of fraction numerator 1 over denominator k open parentheses 2 k plus 1 close parentheses end fraction equals sum from k equals 1 to n of fraction numerator 2 over denominator 2 k open parentheses 2 k plus 1 close parentheses end fraction equals 1 half sum from k equals 1 to n of fraction numerator 1 over denominator 2 k open parentheses 2 k plus 1 close parentheses end fraction equals 1 half sum from k equals 1 to n of open square brackets fraction numerator 1 over denominator 2 k end fraction minus fraction numerator 1 over denominator 2 k plus 1 end fraction close square brackets equals 1 half open square brackets 1 half sum from k equals 1 to n of 1 over k minus sum from k equals 1 to n of fraction numerator 1 over denominator 2 k plus 1 end fraction close square brackets  
Answered by Renu Varma | 11 Mar, 2020, 12:12: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
Expand e^x sin y as Taylor's series near the point (-1 π/4) up to third degree terms
Asked by cubesneha.2005 | 07 Feb, 2024, 12:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
1•4•7+2•5•8+3•6•9+....... find sn
Asked by prashantbharati75 | 29 Sep, 2023, 09:30: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If H is the HM between p and q then h/p+h/q
question image
Asked by mahavenkat152004 | 25 Jul, 2020, 07:49: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
1/1.3+1/2.5 +......+1/n(2n+1)
Asked by kien44123986 | 03 Mar, 2020, 08:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Sum the series to n terms  1.2.4+2.3.7+3.4.10+...
Asked by fishtailfever | 10 Nov, 2019, 12:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Sum of term: 1^3+3^3+5^3+7^3....
Asked by vasaya.sohil99 | 24 Sep, 2019, 11:16: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
PLEASE HELP
question image
Asked by Apoorva | 19 Sep, 2018, 10:04: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
15th 
question image
Asked by lovemaan5500 | 12 Jul, 2018, 10:09: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the sum of n terms of the series whose nth term is n2 + 2n.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the sum of the series 1 + (1 + 2) + (1 + 2 + 3) + … up to n terms.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×