CBSE Class 9 Answered
in a rectangle ABCD, E is a point which bisects BC, PROVE that AE = ED.
Asked by nisha_vini29 | 13 Sep, 2015, 12:41: AM

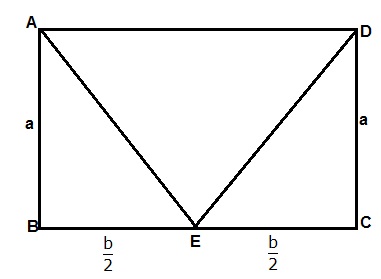

Answered by | 14 Sep, 2015, 06:01: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by rathorgaurav2945 | 21 Apr, 2024, 10:31: PM
CBSE 9 - Maths
Asked by monika.vns14 | 18 Apr, 2024, 05:15: PM
CBSE 9 - Maths
Asked by gulshanelectronics2017 | 15 Apr, 2024, 05:35: PM
CBSE 9 - Maths
Asked by tripura78839 | 12 Apr, 2024, 09:05: PM
CBSE 9 - Maths
Asked by singhanjali0199 | 12 Apr, 2024, 08:29: PM
CBSE 9 - Maths
Asked by killerstealer593 | 11 Apr, 2024, 07:50: PM
CBSE 9 - Maths
Asked by saee.shinde3069 | 31 Mar, 2024, 10:12: PM
CBSE 9 - Maths
Asked by rathoreraj7296 | 31 Mar, 2024, 08:09: PM
CBSE 9 - Maths
Asked by divyanshibirla037 | 29 Mar, 2024, 03:26: PM