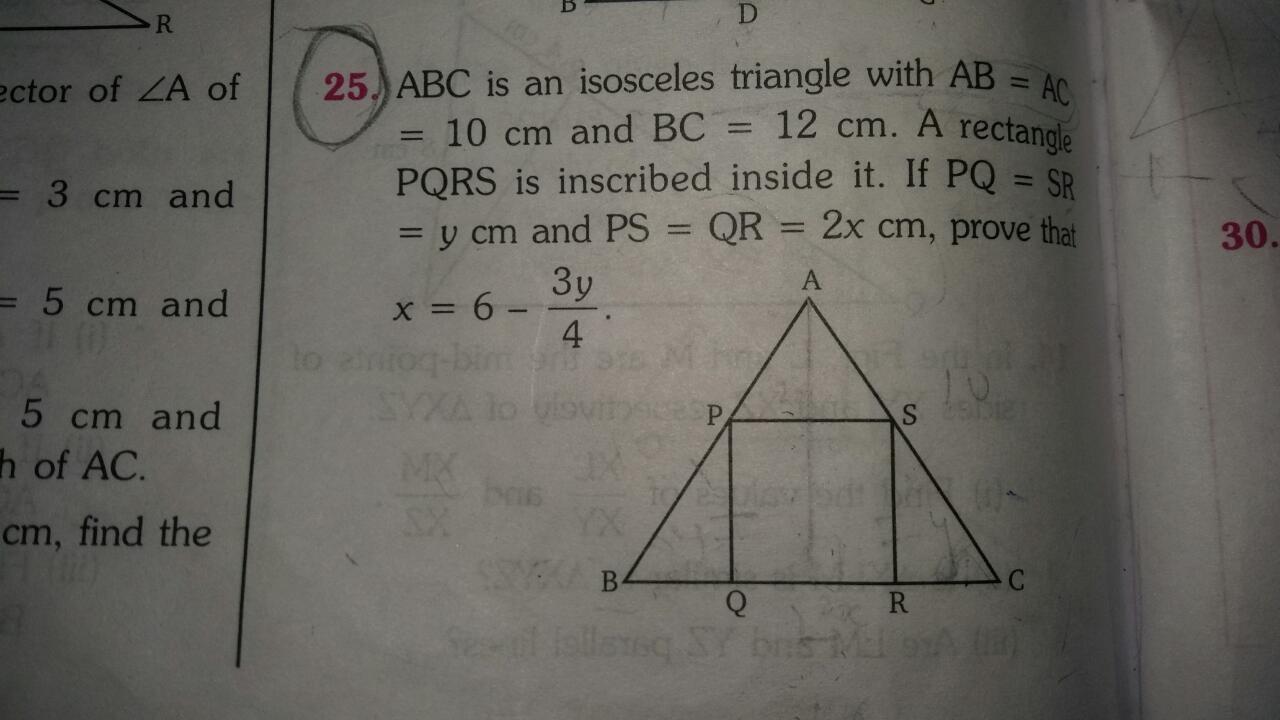ICSE Class 9: Pythagoras Theorem Videos | Deriving Pythagoras Theorem from the concept of similar triangles

• prove by Pythagoras theorem that the diagonal of a rectangle are equal in length
• Pythagoras Theorem  How to solve the problem in the given picture?  
  
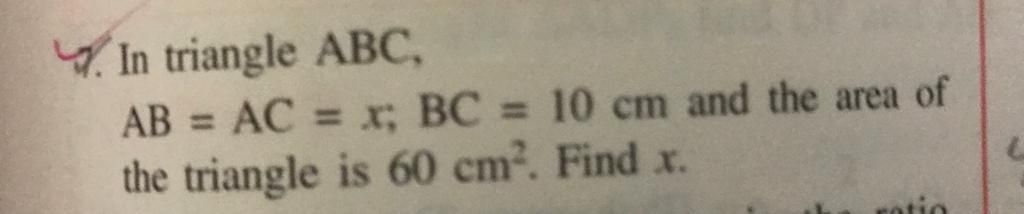
• In triangle ABC, ∠B equals to 90° and D is midpoint of BC. Prove that AC 2 =AD 2 + 3 CD 2
  
• in tringle ABC, angle B is 90 °and D is the mid point of BC . prove that  1. AC² = AD² + 3CD² 2.BC²= 4(AD² -AB²)    
• In rhombus ABCD , prove that : AB^2 + BC^2 + CD^2 + AD^2 = AD^2 + BD^2 
• ABC is a right angled triangle in which ∠ABC = 90° and ∠ACB = 60°. BC is produced to D such that ∠ADB = 45°. If CD = 30 cm, what are the lengths of AB and BC?
• The sides of a right triangle containing the right angle are (5x) cm and (3x-1) cm. If the area of the triangle is 60 cm^2, calculate the length of the sides of the triangle.
• In an isoceles triangle  ABC, AB=AC and D is a point BC produced. Prove that  AD^2=AC^2 + BD * CD
• 1)A man travels 7 km due north ,then goes 3km due east and the 3 km due south.how far is he from starting point  
• 1)The length of two sides of a right angled triangle containing the right angle differ by 6cm.If the area is 36cm2 find the perimeter 2) Solve simultaneously 3/x+4y=7 5/x+6y=13  

Queries asked on Sunday & after 7 pm from Monday to Saturday will be answered after 12 pm the next working day.