CBSE Class 10 Answered
At a point on level ground, the angle of elevation of a vertical tower
is found to be such that its tangent is 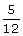 . On walking 192 metres
towards the tower, the tangent of the angle of elevation is
. On walking 192 metres
towards the tower, the tangent of the angle of elevation is 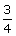 . Find
the height of the tower.
OR
The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. The height of the second tower is 60 m find the height of the first tower.
. Find
the height of the tower.
OR
The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. The height of the second tower is 60 m find the height of the first tower.
Asked by Topperlearning User | 30 Nov, 2013, 02:13: AM
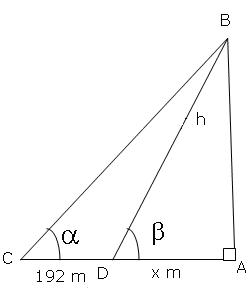
Let AB be the tower of height h metres. Let AD=x metres, CD=192 metres.
tanα = ![]() , tanβ =
, tanβ = ![]()
In ∆BAC,
tanα =![]()
![]()
![]() =
= ![]() ……………………. (i)
……………………. (i)
In ∆DAB,
tanβ = ![]()
![]()
![]() =
= ![]() or x=
or x= ![]() ……………………… (ii)
……………………… (ii)
Using (ii) in (i)
![]() =
= 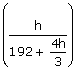
5![]() = 12h
= 12h
2880 +20h =36h
16h = 2880 or h= 180
Hence, the height of the tower is 180 metres.
OR

Let AB and CD be two towers of height h m and 60 m respectively.
AC=140m and ÐBDE =300.
In ∆DEB,
tan 30° = ![]()
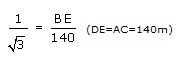
BE =![]() = 80.83m
= 80.83m
Thus, the height of the first tower is
AB= AE+BE = CD+BE =60+80.83 = 140.83m
Answered by | 30 Nov, 2013, 04:13: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by swetalinasamantaray022 | 21 Mar, 2023, 04:15: PM
CBSE 10 - Maths
Asked by badakhsharda | 14 Apr, 2022, 08:57: AM
CBSE 10 - Maths
Asked by naancysingh | 09 Apr, 2022, 07:07: PM
CBSE 10 - Maths
Asked by vy499292 | 23 Jan, 2022, 08:04: PM
CBSE 10 - Maths
Asked by urzashu7818 | 15 Jan, 2021, 12:52: PM
CBSE 10 - Maths
Asked by arindeep.singh | 11 Sep, 2020, 02:41: PM
CBSE 10 - Maths
Asked by debeswar32 | 06 Aug, 2020, 10:55: AM
CBSE 10 - Maths
Asked by ahmadaarif199 | 24 Jul, 2020, 02:58: PM











