CBSE Class 9 Answered
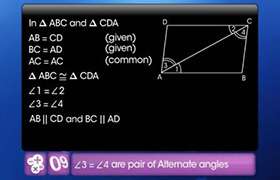
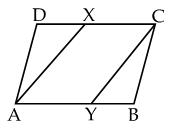
ABCD is a parallelogram and line segments
AX and CY bisect angles A and C. Show that AX||YC.

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
![]() 1
=
1
= ![]() 2,
2, ![]() 3 =
3 = ![]() 4 And
4 And ![]() A=
A=![]() C
C
AD=BC
![]() D=
D=![]() B
B
![]() (by ASA rule)
(by ASA rule)
DX
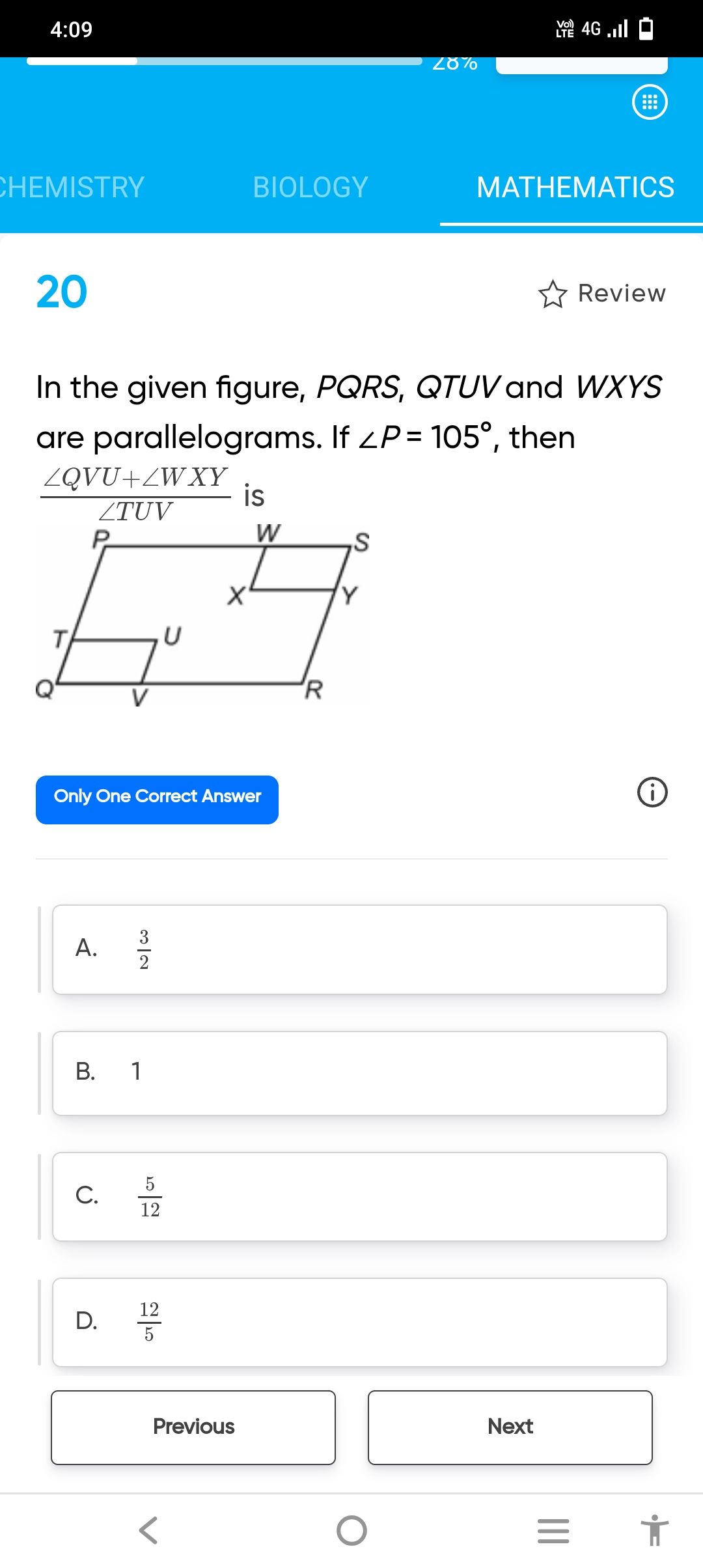
= BY ![]() BY = DX
BY = DX
AB = CD
AB - BY = DC - DX
AY = CX
AY||CX
![]() AYCX is a parallelogram
AYCX is a parallelogram
![]() AX||CY
AX||CY
OR,
![]() A =
A = ![]() C
C
(Opposite angles of parallelogram ABCD)
Therefore,
![]()
![]() A =
A = ![]()
![]() C
C
i.e., ![]() YAX =
YAX = ![]() YCX …(1)
YCX …(1)
Also, ![]() AYC +
AYC + ![]() YCX = 180º (Because YA || CX)…. (2)
YCX = 180º (Because YA || CX)…. (2)
Therefore,
![]() AYC +
AYC + ![]() YAX = 180º [From (1) and (2)]
YAX = 180º [From (1) and (2)]
So, AX || CY (As interior angles on the same side of the transversal are supplementary)
Answered by | 04 Jun, 2014, 03:23: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
CBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
CBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
CBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
CBSE 9 - Maths
Asked by vidyakashid7578 | 20 Sep, 2020, 01:36: AM
CBSE 9 - Maths
Asked by dvmathur | 22 Nov, 2019, 02:42: PM
CBSE 9 - Maths
Asked by prakash.sanyasi | 31 Oct, 2019, 11:27: PM
CBSE 9 - Maths
Asked by prakash.sanyasi | 21 Oct, 2019, 04:03: PM
CBSE 9 - Maths
Asked by Topperlearning User | 16 Aug, 2017, 03:08: PM
CBSE 9 - Maths
Asked by Topperlearning User | 16 Aug, 2017, 03:09: PM