Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

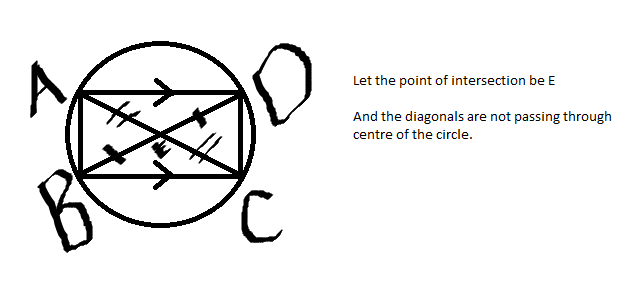
This Question is from chapter Quadrilaterals. EXPERTS, PLEASE ANSWER THIS AS SOON AS POSSIBLE If APB and CQD are two parallel lines then find the type of quadrilateral formed by the bisectors of the angles APQ, CPQ, QCP, and PQD.
Asked by prakash.sanyasi | 31 Oct, 2019, 11:27: PM
Expert Answer
The question should be:
If APB and CQD are two parallel lines then find the type of quadrilateral formed by the bisectors of the angles APQ, BPQ, CQP, and PQD
L e t space X space a n d space Y space b e space t h e space i n t e r s e c t i o n space o f space b i s e c t o r s space o f space a n g l e s space A P Q comma space C Q P space a n d space a n g l e s space B P Q comma space P Q D space r e s p e c t i v e l y G i v e n colon space A P B space vertical line vertical line space C Q D rightwards double arrow angle A P Q equals angle P Q D space.... space A l t e r n a t e space a n g l e s rightwards double arrow angle X P Q equals angle P Q Y therefore space P X space vertical line vertical line space Q Y S I m i l a r l y comma space angle Q P Y equals angle P Q X therefore space Q X space vertical line vertical line space P Y therefore space P X Q Y space i s space a space p a r a l l e log r a m C Q D space i s space a space l i n e rightwards double arrow angle C Q P plus angle P Q D equals 180 degree rightwards double arrow 2 angle P Q X plus 2 angle P Q Y equals 180 degree rightwards double arrow angle P Q X plus angle P Q Y equals 90 degree rightwards double arrow angle X Q Y equals 90 degree therefore space angle X P Y equals 90 degree rightwards double arrow space angle P X Q equals 90 degree space a n d space angle P Y Q equals 90 degree H e n c e comma space P X Q Y space i s space a space r e c tan g l e.
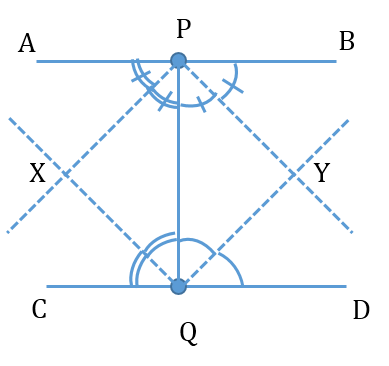
Answered by Renu Varma | 01 Nov, 2019, 10:19: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
Please solve in fast
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
what is ASA congruence rule
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
ABCD is a trapezium in which ab is parallel to cd and ad is equal to bc
Asked by vidyakashid7578 | 20 Sep, 2020, 01:36: AM
ANSWERED BY EXPERT
CBSE 9 - Maths
IN TRIANGLE PQR,  ANGLE PQR =90 DEGREE  PR=10CM  S IS MIDPOINT OF PR. FIND LENGTH OF QS.
Asked by dvmathur | 22 Nov, 2019, 02:42: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
This Question is from chapter Quadrilaterals. EXPERTS, PLEASE ANSWER THIS AS SOON AS POSSIBLE If APB and CQD are two parallel lines then find the type of quadrilateral formed by the bisectors of the angles APQ, CPQ, QCP, and PQD.
Asked by prakash.sanyasi | 31 Oct, 2019, 11:27: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
This question is from CIRCLE chapter and the topic for this related question is CYCLIC QUADRILATERALS AC and BD are two chords of a circle which bisects each other. Prove that  (i) AC and BD are diameters of the circle (ii) ABCD is a rectangle  
Asked by prakash.sanyasi | 21 Oct, 2019, 04:03: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the diagonals of a rhombus are perpendicular to each other.
Asked by Topperlearning User | 16 Aug, 2017, 03:08: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
In the figure PQRS is a parallelogram and X, Y are the points on the diagonal QS, such that SX = QY. Prove that quadrilateral PYRX is a parallelogram.
Asked by Topperlearning User | 16 Aug, 2017, 03:09: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
ABCD is a parallelogram and E is the mid point of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.
Asked by Topperlearning User | 16 Aug, 2017, 03:09: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
ABCD is a parallelogram. E and F are the mid points of the sides AB and CD respectively. Prove that the segments CE and AF trisect the diagonal BD.
Asked by Topperlearning User | 16 Aug, 2017, 03:10: PM
ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt