CBSE Class 9 Answered
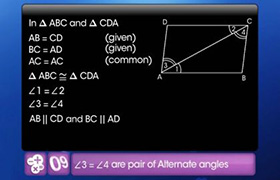
In the figure PQRS is a parallelogram and X, Y are the points on the diagonal QS, such that SX = QY. Prove that quadrilateral PYRX is a parallelogram. 
Asked by Topperlearning User | 16 Aug, 2017, 15:09: PM
Expert Answer
Join PR
OQ = OS (diagonals of a parallelogram bisect each other)
QY = SX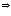
OQ - QY = OS - SX
OY = OX
In quadrilateral PXRYAO = OX
OX =OY
Thus, the diagonals of the quadrilateral
PXY are bisecting each other
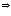PXRY is a parallelogram.
Answered by | 16 Aug, 2017, 17:09: PM
Application Videos
-
Properties of a Parallelogram
This video contains a question which is solved using the property of a para... -
Relation between Parallelogram and Triangle ...
This video explains the relation between the parallelogram and the triangle...
Concept Videos
-
Parallelograms: Basic Properties
This video explains the basics properties of a parallelogram. -
Problem solving on properties related to parallelograms ...
This video explains problem solving approaches related to parallelograms. -
Parallelograms: Basic Properties
Parallelograms:Basic Properties
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 19:24: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 16:17: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by vidyakashid7578 | 20 Sep, 2020, 01:36: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by dvmathur | 22 Nov, 2019, 14:42: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by prakash.sanyasi | 31 Oct, 2019, 23:27: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by prakash.sanyasi | 21 Oct, 2019, 16:03: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Topperlearning User | 16 Aug, 2017, 15:08: PM
ANSWERED BY EXPERT
