CBSE Class 10 Answered
A round balloon of radius r subtends an angle 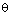 at the eye of the
observer while the angle of elevation of its centre is
at the eye of the
observer while the angle of elevation of its centre is 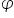 . Prove that the
height of the centre of the balloon is
. Prove that the
height of the centre of the balloon is  .
.
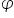 . Prove that the
height of the centre of the balloon is
. Prove that the
height of the centre of the balloon is  .
.
Asked by Topperlearning User | 02 Dec, 2013, 01:34: AM
 k
k
Let O be the centre of the balloon of radius r and P the eye of the observer. Let PA and PB be tangents from P to the balloon. 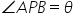 .
.
Therefore, 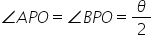
Let OL be perpendicular from O to the horizontal.
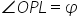
In ∆OAP,
sin![]() =
= ![]()
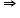 OP= r cosec
OP= r cosec![]() …(i)
…(i)
In ∆OPL,
sinф = ![]()
 OL=OP sinф
OL=OP sinф
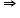 OL = r sinф cosec
OL = r sinф cosec![]() (from (i))
(from (i))
Thus, the height of the centre of the balloon is r sinф cosec![]() .
.
Answered by | 02 Dec, 2013, 03:34: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by swetalinasamantaray022 | 21 Mar, 2023, 04:15: PM
CBSE 10 - Maths
Asked by badakhsharda | 14 Apr, 2022, 08:57: AM
CBSE 10 - Maths
Asked by naancysingh | 09 Apr, 2022, 07:07: PM
CBSE 10 - Maths
Asked by vy499292 | 23 Jan, 2022, 08:04: PM
CBSE 10 - Maths
Asked by urzashu7818 | 15 Jan, 2021, 12:52: PM
CBSE 10 - Maths
Asked by arindeep.singh | 11 Sep, 2020, 02:41: PM
CBSE 10 - Maths
Asked by debeswar32 | 06 Aug, 2020, 10:55: AM
CBSE 10 - Maths
Asked by ahmadaarif199 | 24 Jul, 2020, 02:58: PM











