CBSE Class 9 Maths Properties of Isosceles Triangle
-
Properties of Isosceles Triangle
Establish the relation between equal sides and angles in a triangle. Apply -
Properties of Isosceles Triangle
Establish the relation between equal sides and angles in a triangle. Apply -
Properties of Isosceles Triangle
Establish the relation between equal sides and angles in a triangle. Apply
- the perimeter of an equilateral triangle is 72 M find its area
-
triangle ABC is an equilateral triangle, AB = 6cm. the points P,Q and R are midpoints of AB BC, CA respectively . the perimeter of ? PBCR is
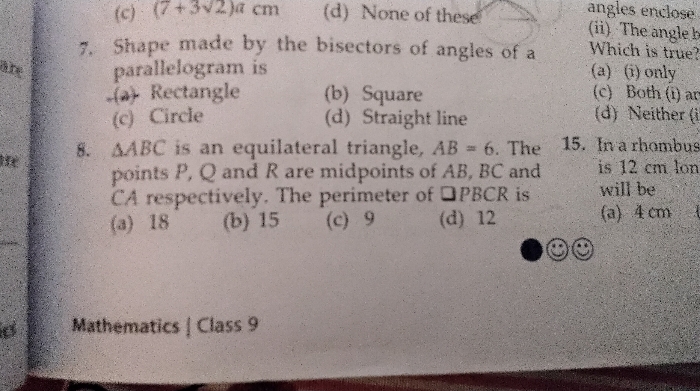
- the area of an equilateral triangle is 49?3 sq.cm, it's perimeter is
- M is a point inside a square ABCD. AMCD is equilateral triangle and MC cuts diagonal DB at E. Then, ZBEC=..... (1) 75° (3) 105° (2) 90° (4) 60°
- In fig. 12.116 , T is a point on the side QR of ? PQR and S is a point such that RT=St. Prove that PQ+PR>QS
- In the figure, ABCD is a square and PAB is a triangle such that AQ = BR. Prove that DPQR is an isosceles triangle.
- If the vertex angle of an isosceles triangle is 50° ,find the other angels
-
show that BX=CY.
- AD is an altitude of an isosceles triangle ABC in which AB=AC.Show that ( i )AD bisects BC (ii) AD bisects angle A.
- If the segments drawn perpendicular to the two sides of a triangle from the mid point of the third side be congruent and equally inclined to the third side, prove that the triangle is isosceles.
