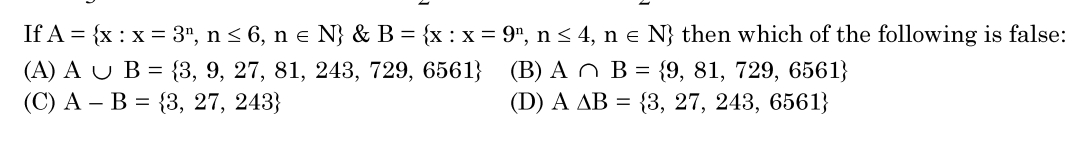CBSE Class 11-science Answered
what will be the cofficient of x^16 & x^17 in the expension (x+1)(x+2)(x+3)(x+4)..........(x+18)???
Asked by Piyush Gupta | 20 Oct, 2010, 12:00: AM
Expert Answer
The coefficient of x17 in the expression (x+1)(x+2)(x+3)(x+4)..........(x+18) will be given by
Sum of 1,2,3.................18
So, coefficient of x17 = 1+2+3+.....18
Sum of n natural numbers is given by 
coefficient of x17 = 171
Coefficent of x16 = sum of product of roots taken two at a time
= (1.18 + 1.17 + 1.16..........1.2)+(2.18+2.17..........2.3) + ............+ 17(18)
= 18(1+2+.....17)+17(1+2+3........16)+16(1+2+3.....15)+..............+.2(1)
Solve the above expression by using the formula for sum of n natural numbers to get the value of coefficient of x16
Answered by | 22 Oct, 2010, 12:25: PM
Concept Videos
-
Types of sets and its representation
Types of sets and describe two forms of set representation. -
Subsets and Supersets
This video covers the definition of subsets and supersets of a set and also... -
Representing the union and intersection of sets
Venn diagrams. Represent the union and intersection of sets with the help o... -
Algebra of Sets
This video explains the concept of the difference of two given sets and rep... -
Counting Theorems ...
This video explains the application of set theory and Venn diagram to solve...
CBSE 11-science - Maths
Asked by parvanipatil09 | 29 Mar, 2024, 10:12: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by divyanshtikkiwal6 | 23 Feb, 2024, 07:44: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by pranavsrinivas82 | 14 Jan, 2024, 07:45: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by pranavsrinivas82 | 10 Jan, 2024, 08:45: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by naiduuofficial | 06 Jan, 2023, 07:49: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by anjaneyagadgil04 | 05 Jan, 2023, 12:16: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by bangtan7hybe | 18 Sep, 2022, 06:36: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by kdimple765 | 24 Jun, 2022, 04:22: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by arjunsah797 | 03 Mar, 2022, 06:04: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by krishkhare04 | 03 Feb, 2022, 02:35: PM
ANSWERED BY EXPERT
