CBSE Class 12-science Answered
Verify Rolle's theorem for each of the following functions on indicated intervals :
f (x) = sin x – sin 2 x on [0, p]
Asked by Topperlearning User | 04 Aug, 2014, 16:35: PM

Answered by | 04 Aug, 2014, 18:35: PM
Concept Videos
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 15:57: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 16:00: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 16:03: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 16:11: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 05 Aug, 2014, 08:38: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 15:32: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 15:48: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 16:16: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 16:35: PM





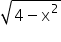 on [– 2, 2].
on [– 2, 2].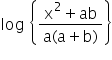 on [a, b], where 0 < a < b.
on [a, b], where 0 < a < b.