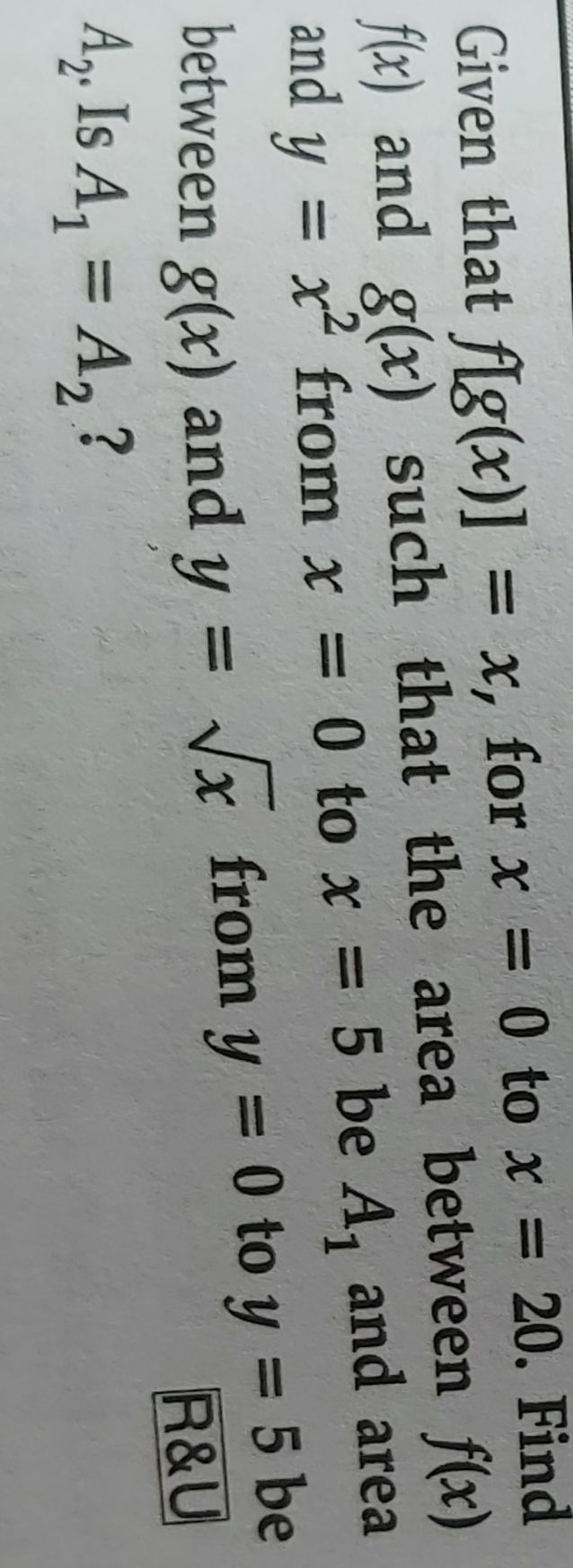Ask a Doubt

Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

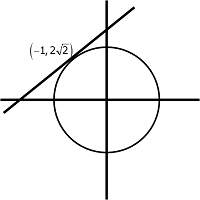
<div>Using integration find the area of triangle formed by -ve x axis,the tanget and normal to the circle x</div> <div>^2+y^2=9 at the point (-1,2* 2^1/2)</div>

Asked by Balbir | 29 Nov, 2017, 10:13: PM

Expert Answer

$begin mathsize 16px style tangent space to space std space circle space is space given space by space straight y equals mx plus-or-minus straight r square root of 1 plus straight m squared end root now space straight r equals 3 comma space straight y equals 2 square root of 2 comma space straight x equals negative 1 we space get 8 straight m squared minus 4 square root of 2 straight m plus 1 equals 0 straight m equals fraction numerator square root of 2 over denominator 4 end fraction now space you space can space find space the space ans space using space geometry so space equation space of space line space is straight y equals fraction numerator square root of 2 over denominator 4 end fraction straight x plus 8 square root of 1 plus open parentheses fraction numerator square root of 2 over denominator 4 end fraction close parentheses squared end root space consider space plus straight r space since space 3 rd space quadrant y equals fraction numerator square root of 2 over denominator 4 end fraction straight x plus 6 square root of 2 end style$

begin mathsize 16px style finding space the space straight x space intercept space and space straight y space intercept space and space applying space 1 half cross times straight b cross times straight h OR thru space integration integral subscript negative 24 end subscript superscript 0 open parentheses fraction numerator square root of 2 over denominator 4 end fraction straight x plus 6 square root of 2 close parentheses end style

.

Answered by Arun | 30 Nov, 2017, 01:14: PM

Practice Test

Pre Board Assessment

Concept Videos

Answered Unanswered My Questions My Answers

CBSE 12-science - Maths

y=cos x and y=1-2x/π

Asked by prasannavvss5 | 27 Sep, 2020, 01:00: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Pl ans

Asked by jain.pradeep | 01 Dec, 2019, 04:31: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the area between x axis, x^2 + y^2 = 8x and y^2 = 4x

Asked by bjayanta | 20 Nov, 2018, 02:05: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the area of region bounded by

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Using integration find the area bounded by the curves

.

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the area of region bounded by

using integration.

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the area of the circle

exterior to the parabola

.

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the area of the region bounded by the curves x² + y² = 2 and x = y².

Asked by Topperlearning User | 12 Aug, 2016, 09:58: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the area of the smaller region bounded by the curves x² + y² = 4 and y²= 3(2x – 1).

Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Draw a sketch of the curves y = sin x and y = cos x at

and find the area of the region enclosed by them and X-axis.

Asked by Topperlearning User | 12 Aug, 2016, 10:30: PM

ANSWERED BY EXPERT

My Class Videos Tests Plans Ask a Doubt

Start your hassle free Education Franchisee and grow your business!

×