CBSE Class 10 Answered
Using basic proportionality theorem,prove that the line joining the mid points of any two sides of triangle is parallel to the third side and half of it
Asked by Prajyot Tugaonkar | 17 May, 2013, 07:04: PM
Expert Answer
Basic Proportionality Theorem - If a given line passes through the two sides of the given triangle and parallel to the third side, then it cuts the sides proportionally. This is called the Basic Proportionality theorem.
hence, in ABC is a triangle with D, E being the mid points of side AB and AC respectively. (Given)
So, AD/DB = AE/EC = 1
So, by inverse of basic proportionality theorem, DE is parallel to BC
Also, in triangle ABC and ADE
angle A = angle A (common)
Also AD/AB = AE/AC (D, E are mid points of AD and AB respectively)
Hence, ABC ~ ADE (By SAS similarity)
So, AD/AB = AE/AC = DE/BC = 1/2
Hence, DE = 1/2 BC
Answered by | 18 May, 2013, 05:23: AM
Application Videos
-
Application of Basic proportionality theorem ...
This video explains the concept of an isosceles triangle and Basic Proporti... -
Area of a right angled triangle
This video explains how to compute the area of a right angled triangle. -
Word Problem on Pythagoras Theorem
This video explains the concept of Pythagoras Theorem and the area of the r... -
Area of Similar Triangles
The video explains the relation between areas and sides of similar trian...
-
Word Problem on An Equilateral Triangle
The video explains a proof based on equilateral triangle.
Concept Videos
-
Converse of BP theorem
Statement and derivation of the converse of the Basic Proportionality Theor... -
Criteria for similarity of triangles
This video explains the basic criteria for similarity of triangles and unde... -
Revision on concepts related to similar triangles ...
Review concepts related to Similar Triangles and practice problems based on... -
Basic Proportionality Theorem ...
This video explains the statement and derivation of the Basic Proportionali... -
Areas of similar triangles
This video explains the relation between the area of similar triangles and ...
CBSE 10 - Maths
Asked by suryapalsinghgoudmahirajbanna | 17 Sep, 2023, 10:50: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by bnarayanamstr | 03 May, 2023, 10:03: AM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by savitamahajan202 | 30 Dec, 2022, 12:51: PM
ANSWERED BY EXPERT
CBSE 10 - Maths
Asked by bhu.joshi54 | 04 Jul, 2022, 08:18: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by bhu.joshi54 | 16 Jun, 2022, 07:56: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by dishapalnati82 | 24 Nov, 2021, 09:30: AM
ANSWERED BY EXPERTCBSE 10 - Maths
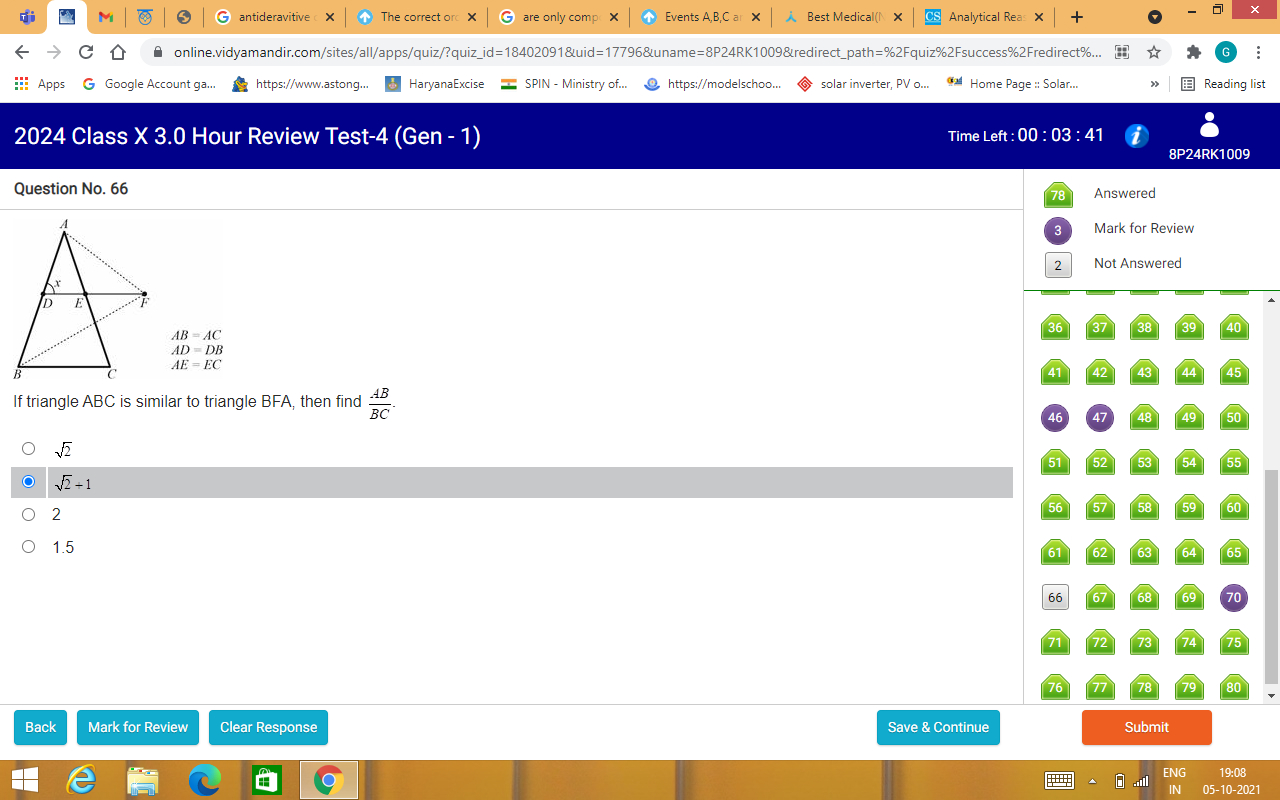
Asked by psinghaladv | 05 Oct, 2021, 07:49: PM
ANSWERED BY EXPERT
