JEE Class main Answered
the kinetic energy of a particle moving along a circle of radius R depends on the distance covered s as KE = as^2 where a is constant . find force acting on particle as function of s
Asked by keshavgoyal9pro | 21 May, 2022, 19:59: PM
Expert Answer
Let us consider a particle starts from rest and attains kinetic energy ( a s2 ) after moving a distance s in circular path
By work-energy theorem , workdone W = ( a s2 )
Force Ft = dW/ds = ( 2 a s )
Above force Ft is acting along tangential direction .
If kineteic energy at a distance s is (a s2 ) , then we get velocity at a distance s as
(1/2) m v2 = a s2 or v2 = ( 2 a s2 ) /m
Radial force ( centripetal force ) , Fr = m ( v2 / R ) = ( 2 a s2 ) / R
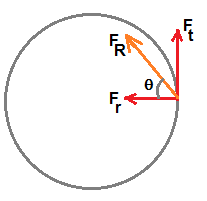
Radial force Fr and tangential force Ft are perpendicular to each other. Hence , resultant force FR is given as
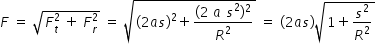
Direction of force makes angle θ with radial force so that , tanθ = Ft / Fr = ( 2 a s ) / [ ( 2 a s2 ) / R ] = ( R / s )
Answered by Thiyagarajan K | 21 May, 2022, 23:31: PM
JEE main - Physics
Asked by sonakshiswami0 | 12 Jun, 2024, 22:29: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by keshavgoyal9pro | 21 May, 2022, 19:59: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by prajwalkambale85 | 17 Feb, 2022, 10:32: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by nimmaka06 | 25 Aug, 2021, 10:32: AM
ANSWERED BY EXPERT