Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

a curve in a speed track has a radius of 150m.there was no lateral friction force exerted on the wheels of a car travelling at 135 km/hr.find the banking angle of track. if the racing car starts skidding when travelling at the speed of 300km/hr.determine the coefficient of static friction between the tyres and track
Asked by nimmaka06 | 25 Aug, 2021, 10:32: AM
answered-by-expert Expert Answer
Maximum speed vmax on a banking road is given as
 
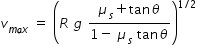begin mathsize 14px style v subscript m a x end subscript space equals space open parentheses R space g space fraction numerator mu subscript s plus tan theta over denominator 1 minus space mu subscript s space tan theta end fraction close parentheses to the power of 1 divided by 2 end exponent space end style................................. (1)
where R is radius of curve, g is acceleration due to gravity , μs is static friction coefficient
and θ is anle of banking

For the First part of the question, let us assume given speed is maximum when there is no friction .
 
Hence if we substitute μs = 0 in above equation ,we get
 
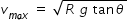begin mathsize 14px style v subscript m a x end subscript space equals space square root of R space g space tan theta end root space end style ..........................(2)
vmax = 135 km/hr = 135 × (5/18) = 37.5 m/s
 
From eqn.(2) , we get , 
 
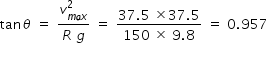begin mathsize 14px style tan theta space equals space fraction numerator v subscript m a x end subscript superscript 2 over denominator R space g end fraction space equals space fraction numerator 37.5 space cross times 37.5 over denominator 150 space cross times space 9.8 end fraction space equals space 0.957 end style .............................(3)
Hence banking angle θ = tan-1 ( 0.957 ) = 43.7o
 
--------------------------------------
 
For second part let us assume friction between tyre and road surface.
 
Given maximum speed vmax = 300 × (5/18) = 83.33 m/s
 
From eqn.(1) we get
 
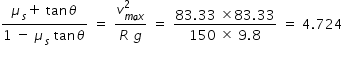
begin mathsize 14px style fraction numerator mu subscript s plus space tan theta over denominator 1 space minus space mu subscript s space tan theta end fraction space equals space fraction numerator v subscript m a x end subscript superscript 2 over denominator R space g end fraction space equals space fraction numerator 83.33 space cross times 83.33 over denominator 150 space cross times space 9.8 end fraction space equals space 4.724 end style
By substituting tanθ = 0.957 in above expression , we get μs = 0.682
Answered by Thiyagarajan K | 25 Aug, 2021, 13:18: PM
Multiple Choice Questions Practice Test
My Class Videos Tests ₹ Plans Ask a Doubt