CBSE Class 10 Answered
The angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of the reflection of the cloud in the lake is 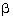 . Prove that the height of the cloud is
. Prove that the height of the cloud is  metres.
OR
From a window, h metres high above the ground, of a house in a street, the angles of elevation and depression of the top and the foot of another house on the opposite side of the street are α and
metres.
OR
From a window, h metres high above the ground, of a house in a street, the angles of elevation and depression of the top and the foot of another house on the opposite side of the street are α and 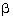 respectively. Show that the height of the opposite house is h(1+tanα cot
respectively. Show that the height of the opposite house is h(1+tanα cot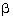 ) metres.
) metres.
Asked by Topperlearning User | 02 Dec, 2013, 10:33: AM
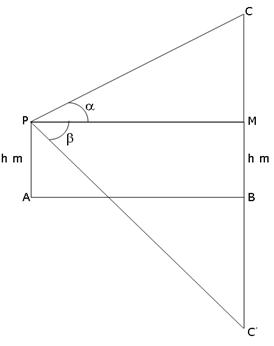
Let C be the cloud and C' be its reflection. Let the height of the cloud be H metres.
BC=BC'=H m
Now BM=AP= h m, therefore, CM= H-h and MC' = H+h
In ![]() CPM,
CPM,
![]() = tan
= tan![]()
![]()
![]() … (i)
… (i)
In ![]() PMC',
PMC',
![]()
![]() … (ii)
… (ii)
From (i) and (ii),
![]()
Htan![]() - htan
- htan![]() = Htan
= Htan![]() +htan
+htan![]()
Htan![]() - Htan
- Htan![]() = htan
= htan![]() + htan
+ htan![]()
H(tan![]() - tan
- tan![]() ) = h(tan
) = h(tan![]() +tan
+tan![]() )
)
![]()
Hence, the height of the cloud is ![]() metres.
metres.
OR
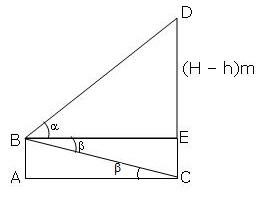
Let B be the window of a house AB and let CD be the other house. Then, AB = EC = h metres.
Let CD = H metres. Then, ED= (H-h) m.
In ![]() BED,
BED,
cot ![]() =
= ![]()
BE = (H-h) cotα … (i)
In ![]() ACB,
ACB,
cot ![]() =
= ![]()
AC=h.cot![]() … (ii)
… (ii)
But BE=AC
![]() (H-h) cot
(H-h) cot![]() = hcot
= hcot![]()
H= ![]()
H = h(1+tan![]() cot
cot![]() )
)
Thus, the height of the opposite house is h(1+tan![]() cot
cot![]() ) metres.
) metres.
Answered by | 02 Dec, 2013, 12:33: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by swetalinasamantaray022 | 21 Mar, 2023, 16:15: PM
CBSE 10 - Maths
Asked by badakhsharda | 14 Apr, 2022, 08:57: AM
CBSE 10 - Maths
Asked by naancysingh | 09 Apr, 2022, 19:07: PM
CBSE 10 - Maths
Asked by vy499292 | 23 Jan, 2022, 20:04: PM
CBSE 10 - Maths
Asked by urzashu7818 | 15 Jan, 2021, 12:52: PM
CBSE 10 - Maths
Asked by arindeep.singh | 11 Sep, 2020, 14:41: PM
CBSE 10 - Maths
Asked by debeswar32 | 06 Aug, 2020, 10:55: AM
CBSE 10 - Maths
Asked by ahmadaarif199 | 24 Jul, 2020, 14:58: PM











