CBSE Class 10 Answered
Sum of first m terms of an A.P. is 0. If a be the first term of the A.P., then the sum of next n terms is :
(A)
1
( )
?
? +
m
a m n m
(B)
1
( )
?
? +
m
a m n n
(C)
1
( )
?
? +
n
a m n n
(D)
1
( )
?
? +
n
a m n m
Asked by snehachauhan0402 | 30 Jul, 2020, 21:50: PM
Sum of first m terms of an AP is 0
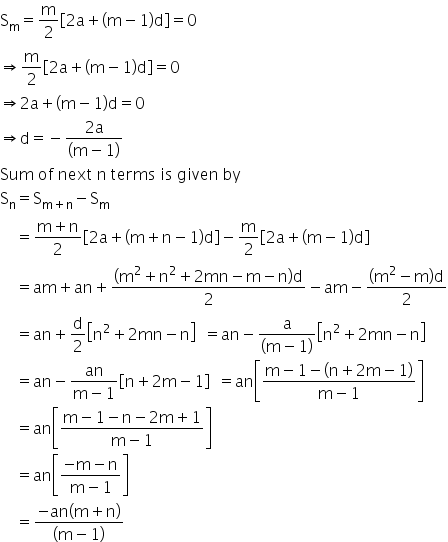
We have
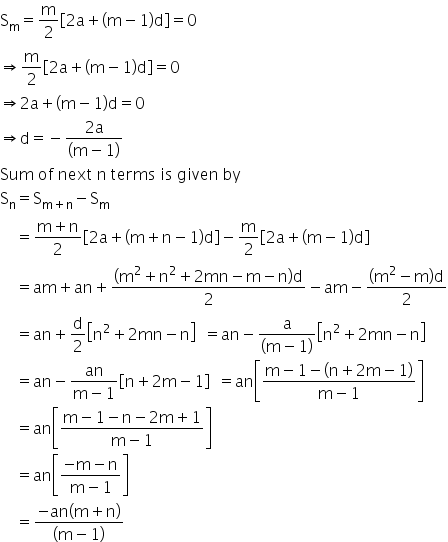
Answered by Renu Varma | 31 Jul, 2020, 11:55: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by lp9128437598 | 10 Jun, 2024, 10:34: AM
CBSE 10 - Maths
Asked by deepikaselvam2009 | 20 Feb, 2024, 20:57: PM
CBSE 10 - Maths
Asked by keshavsinghalhapur | 16 Jan, 2024, 20:46: PM
CBSE 10 - Maths
Asked by keshavsinghalhapur | 15 Jan, 2024, 10:56: AM
CBSE 10 - Maths
Asked by skandachiranjeevin | 06 Dec, 2023, 19:08: PM
CBSE 10 - Maths
Asked by prassanna.j | 13 Nov, 2023, 23:24: PM
CBSE 10 - Maths
Asked by latayadav23 | 17 Oct, 2023, 20:39: PM
CBSE 10 - Maths
Asked by ananya_monica | 28 Sep, 2023, 19:07: PM
CBSE 10 - Maths
Asked by simmysingh1aug | 20 Sep, 2023, 22:20: PM
CBSE 10 - Maths
Asked by bkhaiwangkonyak | 07 Mar, 2023, 16:35: PM












