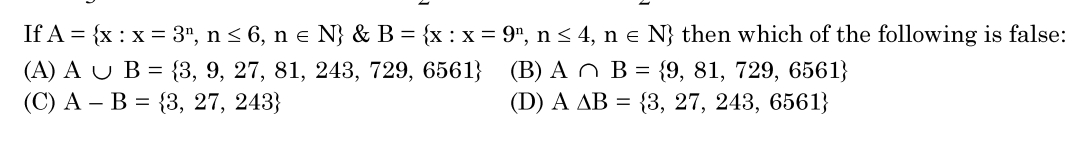CBSE Class 11-science Answered
sir tell me about subsets , & empty sets
Asked by ekanath | 11 Jun, 2009, 11:15: PM
A set A is a subset of a set B if A is "contained" inside B. Notice that A and B may coincide. The relationship of one set being a subset of another is called inclusion.
If A and B are sets and every element of A is also an element of B, then:
-
- A is a subset of (or is included in) B, denoted by
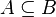 ,
,
- A is a subset of (or is included in) B, denoted by
- or equivalently
- B is a superset of (or includes) A, denoted by

- B is a superset of (or includes) A, denoted by
If A is a subset of B, but A is not equal to B (i.e. there exists at least one element of B not contained in A), then
-
- A is also a proper (or strict) subset of B; this is written as
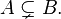
- A is also a proper (or strict) subset of B; this is written as
The empty set is the unique set having no (zero) members. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced. Many possible properties of sets are trivially true for the empty set.
Answered by | 12 Jun, 2009, 04:11: AM
Concept Videos
CBSE 11-science - Maths
Asked by parvanipatil09 | 29 Mar, 2024, 10:12: AM
CBSE 11-science - Maths
Asked by divyanshtikkiwal6 | 23 Feb, 2024, 07:44: PM
CBSE 11-science - Maths
Asked by pranavsrinivas82 | 14 Jan, 2024, 07:45: AM
CBSE 11-science - Maths
Asked by pranavsrinivas82 | 10 Jan, 2024, 08:45: PM
CBSE 11-science - Maths
Asked by naiduuofficial | 06 Jan, 2023, 07:49: PM
CBSE 11-science - Maths
Asked by anjaneyagadgil04 | 05 Jan, 2023, 12:16: PM
CBSE 11-science - Maths
Asked by bangtan7hybe | 18 Sep, 2022, 06:36: PM
CBSE 11-science - Maths
Asked by kdimple765 | 24 Jun, 2022, 04:22: PM
CBSE 11-science - Maths
Asked by arjunsah797 | 03 Mar, 2022, 06:04: PM
CBSE 11-science - Maths
Asked by krishkhare04 | 03 Feb, 2022, 02:35: PM