CBSE Class 11-science Answered
Show that 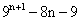 is divisible by 64, whenever n is a positive integer:
is divisible by 64, whenever n is a positive integer:
Asked by Topperlearning User | 30 Sep, 2016, 09:29: PM
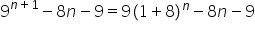
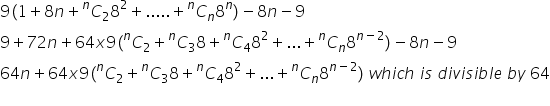
Hence, 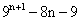 is divisible by 64.
is divisible by 64.
Answered by | 30 Sep, 2016, 11:29: PM
Concept Videos
CBSE 11-science - Maths
Asked by dseno1741 | 29 Mar, 2024, 08:47: PM
CBSE 11-science - Maths
Asked by Manjeet | 23 Mar, 2024, 09:41: PM
CBSE 11-science - Maths
Asked by urvithakur013 | 07 Feb, 2024, 08:56: PM
CBSE 11-science - Maths
Asked by pjthanukeerthy | 10 Dec, 2023, 07:02: AM
CBSE 11-science - Maths
Asked by gdeadshot85 | 12 Jan, 2023, 10:32: AM
CBSE 11-science - Maths
Asked by srp.sumukh | 26 Dec, 2020, 03:34: PM
CBSE 11-science - Maths
Asked by sailaxmareddy123 | 23 Aug, 2020, 10:38: PM
CBSE 11-science - Maths
Asked by gaveshjain355 | 04 Apr, 2020, 11:35: AM
CBSE 11-science - Maths
Asked by Jaibir642 | 10 Sep, 2019, 07:58: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM